Finding current in circuits with inductors and capacitors

[Cocoleia]

Homework Statement

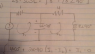
I am practicing these types of problems, for example:

and I am asked to find i(t) in this case, and it is in steady state. I really need someone to walk me through these types of problems, how do I get them started.

Homework Equations

The Attempt at a Solution

I am really unsure of what to do for these types of problems. My best guess would be to replace the inductor with a short circuit, and then calculate the voltage. After replace the capacitor with an open circuit and hopefully be able to find something else, maybe the current? I just need some help with the first steps of these kind of problems

 

[Cutter Ketch]

As the voltage is time varying you won't be looking for a steady state solution.

However, if the voltage was D.C. And you were looking for a steady state solution what you describe is correct. Capacitors are open, inductors are shorted and you calculate from what's left. Of course, what's left is just a voltage across a resistor, so they would never give you a problem like this and ask for the steady state condition.

 

[Cutter Ketch]

So, for relevant equations, what do you know that you think might apply here?

 

[Cocoleia]

So, for relevant equations, what do you know that you think might apply here?

Well, in the question they say it's steady state (The question isn't in English but I believe I am translating it right)
If it's not then I guess I have the equations:
i=Cdv/dt and v = 1/C integral i dt

 

[gneill]

Hi Cocoleia,

The term "steady state" is okay here. It assumes that the AC source has been in operation effectively forever so that any transients associated with switching it on have long since died away and the circuit is responding purely to the AC stimulation of the source.

There are a couple of basic approaches depending upon where you are in your course of study. The first is to write differential equations for the circuit and solve them for the desired quantities. The second (usually introduced a bit later) is more common and involves the use of phasor quantities. It's actually considerably easier than the differential equation approach in the long run. The phasor approach uses complex numbers to represent circuit values such as voltage, current, and impedance. Then the circuit can be solved using all the standard methods you'd apply to DC circuits containing only resistors. Of course all the math is done using complex arithmetic.

You'll have to tell us what approach you are expected to use.

 

[Cocoleia]

Hi Cocoleia,

The term "steady state" is okay here. It assumes that the AC source has been in operation effectively forever so that any transients associated with switching it on have long since died away and the circuit is responding purely to the AC stimulation of the source.

There are a couple of basic approaches depending upon where you are in your course of study. The first is to write differential equations for the circuit and solve them for the desired quantities. The second (usually introduced a bit later) is more common and involves the use of phasor quantities. It's actually considerably easier than the differential equation approach in the long run. The phasor approach uses complex numbers to represent circuit values such as voltage, current, and impedance. Then the circuit can be solved using all the standard methods you'd apply to DC circuits containing only resistors. Of course all the math is done using complex arithmetic.

You'll have to tell us what approach you are expected to use.

I am expected to use the phasor approach

 

[gneill]

Okay, then you'll need to examine the circuit and determine the frequency of the source and the impedances of the reactive components. What do you find?

 

[Cocoleia]

Okay, then you'll need to examine the circuit and determine the frequency of the source and the impedances of the reactive components. What do you find?

 

[gneill]

Good. Pencil in those impedance values on your circuit diagram next to their components. Choose an analysis method and use those values as you would resistance values. Yes, the complex arithmetic will be tedious and a pain, so you might want to do the bulk of the equation solving symbolically and only plug in numbers at the end

 

[Cocoleia]

Good. Pencil in those impedance values on your circuit diagram next to their components. Choose an analysis method and use those values as you would resistance values. Yes, the complex arithmetic will be tedious and a pain, so you might want to do the bulk of the equation solving symbolically and only plug in numbers at the end

I separated it into two loops, for the left loop I got the equation
4-2I₁j+2I₂j+I₁=0
And for the right loop:
2I₁j+6I₂j+4₂=0

 

[gneill]

Check the signs in your first loop equation. The second equation looks okay to me.

 

[Cocoleia]

Check the signs in your first loop equation. The second equation looks okay to me.

Ok, would it be
4+2I1j+2I2j+I1=0

 

[gneill]

I don't think so. How did you define the directions of the two mesh currents?

 

[Cocoleia]

I don't think so. How did you define the directions of the two mesh currents?

 

[gneill]

Ah. Okay, I apologize. I had initially thought that you'd defined them as clockwise currents. So your original loop 1 equation in post #10 is in fact okay. Sorry for wasting your time

 

[Cocoleia]

Ah. Okay, I apologize. I had initially thought that you'd defined them as clockwise currents. So your original loop 1 equation in post #10 is in fact okay. Sorry for wasting your time

No, it's fine. I guess I should define them as being clockwise in the future it will be easier.
What do I do now that I have these equations ?

 

[gneill]

No, it's fine. I guess I should define them as being clockwise in the future it will be easier.
What do I do now that I have these equations ?

I thought you'd choose clockwise in order to make $i_2$ match the direction of the defined inductor current. Otherwise the choice of direction doesn't matter much in the long run.

You'll have to solve the simultaneous equations to find the currents. In particular you'll need to find $i_2$.

 

[Cocoleia]

I thought you'd choose clockwise in order to make $i_2$ match the direction of the defined inductor current. Otherwise the choice of direction doesn't matter much in the long run.

You'll have to solve the simultaneous equations to find the currents. In particular you'll need to find $i_2$.

And once I solve for I2, that will be my answer right ?

 

[gneill]

And once I solve for I2, that will be my answer right ?

Yes, once you sort out the direction difference between of $i_2$ and the inductor current. Oh, and if they want the answer in the time domain (a cosine function of t) then you'll have to convert the phasor result accordingly.

 

[Cocoleia]

Yes, once you sort out the direction difference between of $i_2$ and the inductor current. Oh, and if they want the answer in the time domain (a cosine function of t) then you'll have to convert the phasor result accordingly.

What do you mean by the direction difference?

 

[gneill]

What do you mean by the direction difference?

Your $i_2$ is defined to be counterclockwise. It flows against the direction of $i(t)$ as defined on your circuit diagram.

 

[Cocoleia]

Your $i_2$ is defined to be counterclockwise. It flows against the direction of $i(t)$ as defined on your circuit diagram.

Ok, so I should switch the equation for that loop to be:
-2I₁j-6₂j-4₂
and then solve for I2, and convert if necessary and that will be the final answer ?

 

[gneill]

Ok, so I should switch the equation for that loop to be:
-2I₁j-6₂j-4₂
and then solve for I2, and convert if necessary and that will be the final answer ?

No need to go to all that work. Just negate your result to reverse the direction of the current.