Finding Current in Resistors & Charge of Capacitor

[ananonanunes]

Homework Statement

_

Relevant Equations

_

Suppose the switch has been closed for a long time so that the capacitor is fully charged and current is constant.
a)Find the current in each resistor and charge Q of the capacitor.
b)The switch is now opened at t=0s. Write the equation for the current for the resistor of 15kΩ as a function of time and find the time interval needed for the charge to drop to 1/5 of its original value.

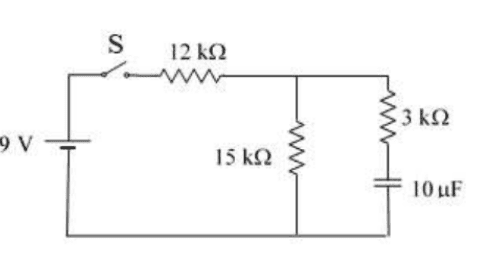
I was able to find the current in the resistors. I assumed the current would be 0A in the resistor of $3k\Omega$ and since there is no current in this "branch", the other two resistors are in series so $I_{R_1}=I_{R_2}$ and $R_{eq}=12+15=27k \Omega$. $I=\frac{\mathcal{E}}{R_{eq}}=333mA$.
I don't know how to find the charge in the capacitor. I thought that, because it was fully charged, $Q=C\mathcal{E}$ but that is not the correct answer.

 

[kuruman]

$Q=CV.$
What do you think the voltage across the capacitor is? Hint: There is no current through the 3 kΩ resistor.

 

[ananonanunes]

$Q=CV.$
What do you think the voltage across the capacitor is? Hint: There is no current through the 3 kΩ resistor.

Since there is no current through the $3k\Omega$ there is also no voltage across that resitor. So I thought the voltage across the capacitor would be the same as the electromotive force, because the voltage wouldn't need to be "split" between the capacitor and the resistor. But this is incorrect and I don't really understand why.

 

[kuruman]

Since there is no current through the $3k\Omega$ there is also no voltage across that resitor. So I thought the voltage across the capacitor would be the same as the electromotive force, because the voltage wouldn't need to be "split" between the capacitor and the resistor. But this is incorrect and I don't really understand why.

Look at the circuit again. The voltage across the capacitor is the same as the voltage across the 15kΩ resistor. What is that voltage?

 

[ananonanunes]

Look at the circuit again. The voltage across the capacitor is the same as the voltage across the 15kΩ resistor. What is that voltage?

I just calculated the voltage and the charge using that voltage and I got the correct result. Thank you so much for the help!