Finding eigenvalues for 4 DOF system

[Sirsh]

Hey all,

I've derived a fourth order dynamic system as represented by the following:

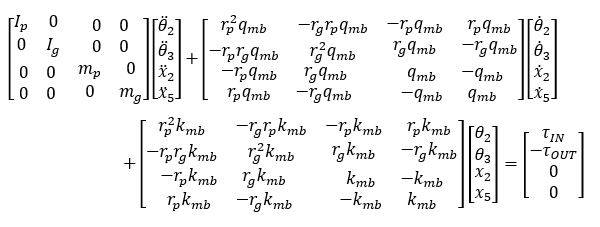
I need to determine the eigenvalues for this system to check whether they're purely real with no imaginary components.

How should I go about doing this? I have done eigenvalue problems in the past, but not to this extent. Would I just determine the eigenvalues for each matrix then do the addition of them?

Note: all the variables (excluding theta's and x's) have constant values.

Any help would be appreciated, thanks!

 

[jambaugh]

Here's how I would approach it, first introduce auxiliary variables and reduce the system to first order. For example replace \ddot{\theta}_2 \to \dot{\omega}_2 and \dot{\theta}_2 \to \omega with the additional equation \dot{\theta}_2 = \omega_2. You'll end up with an 8x8 system but it will be first order, of the form:

\dot{\mathbf{u}} = A \mathbf{u} + \mathbf{b}
With \mathbf{u} = ( \theta_2,\theta_3, x_2, x_5, \omega_2,\omega_3, v_2,v_5)^T.

You can then focus on finding or qualifying the eigen-values of the matrix A.

 

[Sirsh]

Here's how I would approach it, first introduce auxiliary variables and reduce the system to first order. For example replace \ddot{\theta}_2 \to \dot{\omega}_2 and \dot{\theta}_2 \to \omega with the additional equation \dot{\theta}_2 = \omega_2. You'll end up with an 8x8 system but it will be first order, of the form:

\dot{\mathbf{u}} = A \mathbf{u} + \mathbf{b}
With \mathbf{u} = ( \theta_2,\theta_3, x_2, x_5, \omega_2,\omega_3, v_2,v_5)^T.

You can then focus on finding or qualifying the eigen-values of the matrix A.

Thank you for your help Jambaugh!