- 1,753
- 143
Figure 19-38 shows an electron entering a parallel-plate capacitor with a speed of v = 5.25 106 m/s. The electric field of the capacitor has deflected the electron downward by a distance of d = 0.626 cm at the point where the electron exits the capacitor.
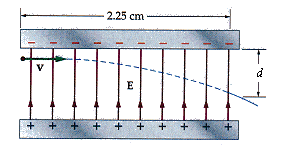
(a) Find the magnitude of the electric field in the capacitor.
b) Find the speed of the electron when it exits the capacitor.
Part A:
E=F/q, but q is not given
F=ma, but m is not given
F=kQq/r2
I don't know where to start.
Part B:
Compute time:
<br /> \begin{array}{l}<br /> t = \frac{d}{v} \\ <br /> \\ <br /> t = \frac{{0.025m}}{{5.25 \times 10^6 m/s}} = 4.2857 \times 10^{ - 8} s \\ <br /> \end{array}<br />
Compute acceleration:
<br /> \begin{array}{l}<br /> y_f = y_i + v_i t + 0.5at^2 \\ <br /> \\ <br /> a = \frac{{y_f - y_i - v_i t}}{{0.5t^2 }} \\ <br /> \\ <br /> a = \frac{{0.626m - 0 - 0t}}{{0.5t^2 }} \\ <br /> \\ <br /> a = \frac{{0.00626m}}{{0.5\left( {4.2857 \times 10^{ - 8} s} \right)^2 }} = 6.81644 \times 10^{12} m/s^2 \\ <br /> \end{array}<br />
Compute velocity:
<br /> \begin{array}{l}<br /> v_{y,f} = v_{y,i} + at \\ <br /> \\ <br /> v_{y,f} = 0 + 6.81644 \times 10^{12} \times 4.2857 \times 10^{ - 8} \\ <br /> \\ <br /> v_{y,f} = 292133.33 \\ <br /> \\ <br /> v_f = \sqrt {v_{y,f}^2 + v_x^2 } \\ <br /> \\ <br /> v_f = \sqrt {(292133.33m/s)^2 + (5.25 \times 10^6 m/s)^2} \\ <br /> \\ <br /> v_f = 5.258122 \times 10^6 m/s \\ <br /> \end{array}<br />
But this answer is wrong.
(a) Find the magnitude of the electric field in the capacitor.
b) Find the speed of the electron when it exits the capacitor.
Part A:
E=F/q, but q is not given
F=ma, but m is not given
F=kQq/r2
I don't know where to start.
Part B:
Compute time:
<br /> \begin{array}{l}<br /> t = \frac{d}{v} \\ <br /> \\ <br /> t = \frac{{0.025m}}{{5.25 \times 10^6 m/s}} = 4.2857 \times 10^{ - 8} s \\ <br /> \end{array}<br />
Compute acceleration:
<br /> \begin{array}{l}<br /> y_f = y_i + v_i t + 0.5at^2 \\ <br /> \\ <br /> a = \frac{{y_f - y_i - v_i t}}{{0.5t^2 }} \\ <br /> \\ <br /> a = \frac{{0.626m - 0 - 0t}}{{0.5t^2 }} \\ <br /> \\ <br /> a = \frac{{0.00626m}}{{0.5\left( {4.2857 \times 10^{ - 8} s} \right)^2 }} = 6.81644 \times 10^{12} m/s^2 \\ <br /> \end{array}<br />
Compute velocity:
<br /> \begin{array}{l}<br /> v_{y,f} = v_{y,i} + at \\ <br /> \\ <br /> v_{y,f} = 0 + 6.81644 \times 10^{12} \times 4.2857 \times 10^{ - 8} \\ <br /> \\ <br /> v_{y,f} = 292133.33 \\ <br /> \\ <br /> v_f = \sqrt {v_{y,f}^2 + v_x^2 } \\ <br /> \\ <br /> v_f = \sqrt {(292133.33m/s)^2 + (5.25 \times 10^6 m/s)^2} \\ <br /> \\ <br /> v_f = 5.258122 \times 10^6 m/s \\ <br /> \end{array}<br />
But this answer is wrong.
Last edited: