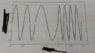Like Tony Stark
- 182
- 6
- Homework Statement
- The picture shows a graph of amplitude (measured in degrees) vs time (measured in seconds) for a pendulum disturbed by different accelerations.
1) Draw the free body diagram of the pendulum in a situtation where this could happen.
2) Find the acceleration for the different periods.
3) When and in which period is the maximun and minimun tension?
4) Find ##\theta (t)## for the region of minimun period and for the following initial conditions: ##\theta _0 =10°##, ##v_o=0.1 rad/s##
- Relevant Equations
- ##x(t)=A.sin(\omega .t)##
Well, this is a problem which makes you think more about concepts than numbers, so I want to see if I've done it correctly.
1) I draw a simple pendulum in an elevator, where you have weight, tension and a pseudo-force. In this situation the effective gravity may be changing due to different accelerations of the elevator so this makes the period change.
2) ##\theta (t)=A.sin(\omega . t)## so differentiating you'll get ##\ddot \theta (t)=-A \omega ^2 sin (\omega .t)##
In this case ##A=\frac{\pi}{180}## and ##\omega## can be easily found knowing the period, then the frequency and then ##\omega##. So you'll get three expressions which will be different just in ##\omega##. I didn't consider ##\phi## because the motion starts at 0
3) The maximun tension is always in the equilibrium point. Then if we think about the situation of the elevator, in this point ##T=mg+f*## where ##f*## is the pseudo-force due to the acceleration of the elevator. Then, if the gravity "is heavier" the period will be minimum, so the tension will be maximum when the period is the smallest.
On the other hand, the tension will be weaker when the pendulum is in the extreme point and when the gravity is "lighter", so when the period is the longest.
4) ##\theta (t) =A.cos(\omega .t + \phi)##. So you have to find ##A## and ##\phi##.
You use ##A=\sqrt{x_0 ^2 +\frac{\dot x_0^2}{\omega^2}}## and ##\phi=arctg(-\frac{\dot x_0}{\omega x_0})##.
So you get the values and replace them.
1) I draw a simple pendulum in an elevator, where you have weight, tension and a pseudo-force. In this situation the effective gravity may be changing due to different accelerations of the elevator so this makes the period change.
2) ##\theta (t)=A.sin(\omega . t)## so differentiating you'll get ##\ddot \theta (t)=-A \omega ^2 sin (\omega .t)##
In this case ##A=\frac{\pi}{180}## and ##\omega## can be easily found knowing the period, then the frequency and then ##\omega##. So you'll get three expressions which will be different just in ##\omega##. I didn't consider ##\phi## because the motion starts at 0
3) The maximun tension is always in the equilibrium point. Then if we think about the situation of the elevator, in this point ##T=mg+f*## where ##f*## is the pseudo-force due to the acceleration of the elevator. Then, if the gravity "is heavier" the period will be minimum, so the tension will be maximum when the period is the smallest.
On the other hand, the tension will be weaker when the pendulum is in the extreme point and when the gravity is "lighter", so when the period is the longest.
4) ##\theta (t) =A.cos(\omega .t + \phi)##. So you have to find ##A## and ##\phi##.
You use ##A=\sqrt{x_0 ^2 +\frac{\dot x_0^2}{\omega^2}}## and ##\phi=arctg(-\frac{\dot x_0}{\omega x_0})##.
So you get the values and replace them.