Finding gain from a bode plot

[snoweangel27]

Homework Statement

Transfer function:
G(s) =$$\frac{k}{s^{2}+2\varsigma\omega_{n}s+\omega_{n}^{2}}$$

a) if u(t) = cos(2t), find the steady state response
b) determine the values for k, damping ratio ($$\varsigma$$), and the natural frequency.

Homework Equations

The Attempt at a Solution

I know how to find the steady state response by finding G(wj) where w = 2 from the input function. However, I can't seem to find the correct values for k, damping ratio, and the natural frequency.

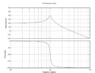
first I found the cut off magnitudes from the bode plot by multiplying the largest magnitude (40) by (1/$$\sqrt{2}$$, to obtain the magnitude of the cut off frequencies to be approx. 28.28db. and found the cut off frequencies to be 8 and 10.1 rad/sec, which allows the Bandwidth to be determined by subtracting the two cut off frequencies.

I believe the natural frequency should be 10, since it is also the center frequency, and I found the damping ration to be 0.105 by dividing the bandwidth by 2 times the natural frequency. And I think the gain should be 10.

my transfer function
G(s) =$$\frac{10}{s^{2}+2.1s+100}$$

when I find the bode plot of this function it looks similar to the provided plot, but the magnitude is off.

 

[Päällikkö]

It's been a while I've done these, hopefully I'm not terribly wrong here as it's not quite my area of specialty. At least I got the image plotted in Matlab and it is indeed exactly the same.

Anyway, setting s = 0, you immediately see that the low pass gain ought to be k/w_n^2. Yours is 1/10, which, if my math is right, gives -20 dB gain rather than 20 dB as shown in the figure.

Phase -90 is quite special. Use that to get a second relation between the parameters. Finally I'd proceed to check what value and where |G| gets as its maximum to find the third and last relation between the parameters. You ought to get nice integers as answers (well, the damping parameter is a reciprocal of one).