Engineering Bode Plot Slope based on frequencies

[guyvsdcsniper]

Homework Statement

Give numerical values of ω that define the ranges where ω can be written as a power law and give the Bode-plot slope in each range, using decibels per dec or oct

Relevant Equations

db=log(v2/v1)

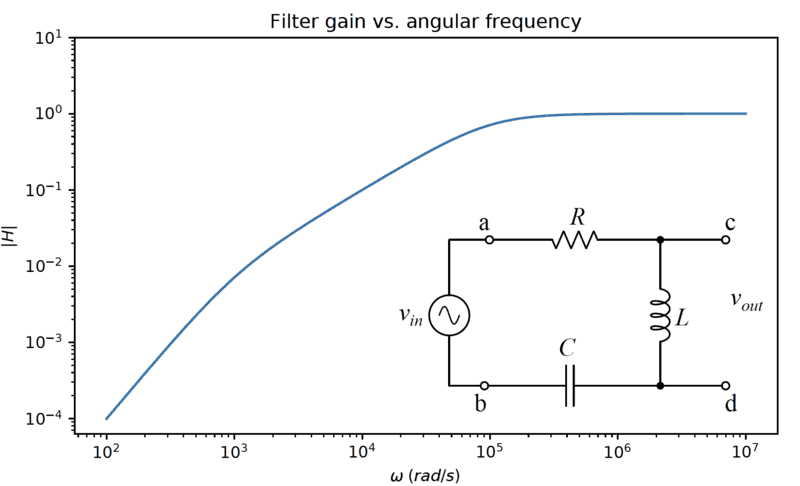
From 0 to $10^3$ $\omega$ there is a dB gain, from $10^3$ to $10^5$ there is another. Finally from $10^5$ to infinity the slope is constant (0).

I know the formula
$$dbV= 20log_{10}\frac{V_2}{V_1}$$

can give me the slope but that is in terms of Volts, but I have frequency and the magnitude of the transfer function. I cant find a formula in my book or online to calculate the dB gain with these two.

Is there an approach to determining the slope of each with the information given in the image?

 

[berkeman]

Have you learned the concepts of "poles" and "zeros" yet, and how they affect the transfer function?

 

[guyvsdcsniper]

Have you learned the concepts of "poles" and "zeros" yet, and how they affect the transfer function?

I have, each pole corresponds a 6dB/oct gain.

So i'm guessing I would need to take the magnitude of the transfer function and evaluate in the limit of low mid and high frequencies?

I calculated the transfer function to be:
$$H = \frac{-\omega^2 L C}{j\omega RC-\omega^2 LC+1}$$
and then found its magnitude:
$$\lvert{H}\rvert = \frac{\omega^2 LC}{\sqrt{(\omega^4 LC+(\omega LC)^2-2\omega^2 LC+1}}$$

Am I going to have to take the quadratic equation of the denominator to find the poles?

 

[DaveE]

Am I going to have to take the quadratic equation of the denominator to find the poles?

Basically yes. But since they haven't given you the component values, the real task here is to recognize the various shapes a quadratic frequency response can take and identify where the poles are from the given plot. Look in your lecture notes about constructing a quadratic bode plot using asymptotes.

Hint: Quadratics always have two poles, identifying whether they are real or complex is an important first step in analysis. If they are complex, then you want to get an idea about the damping (or quality factor Q) to proceed. If they are real, you can treat it as two separate 1st order responses combined together.

This article may be helpful, although it doesn't show the plots.
https://www.physicsforums.com/threads/an-engineers-approach-to-the-quadratic-formula.1053797/

 

[DaveE]

Also, this looks like a good treatment of the subject, if you don't like the version from your class.
http://web.cecs.pdx.edu/~tymerski/ECE311_4.pdf