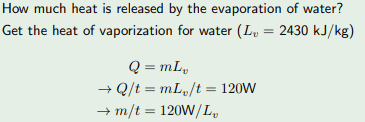SUMMARY
The discussion centers on the heat dynamics involved in the evaporation of water, specifically addressing the misconception that evaporation releases heat. Participants clarify that evaporation requires energy absorption, and thus, heat is drawn from the surrounding environment, including the human body. The mention of "120W" refers to the rate of heat transfer from the body during this process. Understanding these principles is crucial for accurately interpreting thermodynamic interactions in biological systems.
PREREQUISITES
- Basic understanding of thermodynamics
- Knowledge of heat transfer concepts
- Familiarity with the process of evaporation
- Understanding of energy absorption in phase changes
NEXT STEPS
- Research the principles of thermodynamics in biological systems
- Study the heat transfer mechanisms during phase changes
- Explore the concept of latent heat of vaporization
- Investigate the effects of evaporation on human body temperature regulation
USEFUL FOR
Students in physics or biology, researchers in thermodynamics, and professionals in fields related to environmental science or human physiology will benefit from this discussion.