Finding L & C for Circuit Protection: dv/dt & di/dt Values
- Thread starter Johnie
- Start date
-
- Tags
- Circuit Protection
Click For Summary
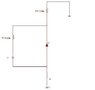
The discussion focuses on determining the appropriate inductance (L) and capacitance (C) values for a circuit protection application involving a thyristor, with specified maximum rates of voltage change (dv/dt) and current change (di/dt). Participants clarify that a snubber circuit is used to protect the thyristor from excessive voltage and current rates, which can lead to unintended conduction or localized heating. The use of Laplace transforms is suggested for analyzing the circuit's behavior, particularly in calculating output voltage and ensuring that chosen L and C values meet the specified di/dt and dv/dt requirements. Additionally, the importance of modeling the thyristor's characteristics, including its on-resistance and parasitic capacitance, is emphasized for accurate analysis. The conversation concludes with suggestions for starting the analysis with basic approximations and considering resonance effects in the circuit.
Similar threads
- · Replies 3 ·
- · Replies 4 ·
- · Replies 12 ·
- · Replies 1 ·
- · Replies 1 ·
- · Replies 3 ·