arestes
- 84
- 4
Homework Statement
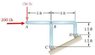
I am given the forces on picture and I´m asked to find the reactions on both supports. I see they are pin supports so they ask me for 4 unknowns.
Homework Equations
Sum of forces in both directions equal to zero
Sum of torques wrt a convenient point equal to zero
THREE equations in total, four unknowns.
The Attempt at a Solution
Sum of forces in both directions equal to zero
Cx+Dx+200=0
Cy+Dy-150=0
Sum of torques wrt "C" equal to zero
3(Dy)-1,5Dx-(3) 200+ (3)150=0
Since I have THREE equations in total, four unknowns. I assumeI need to analyse members separately. I recall that members are supposed to be treated as weightless and subjected to two forces acting on the same line of action if they are part of a truss. However, Member ABC does´nt look like a truss member.
If I analyse pin B I see it can only have horizontal forces acting on it pulling from both sides. Vertically it should have zero force. If I set Cy=0 it leads me to Dx and Dy not being zero both of them and I discovera contradictions if I analyse the member BD because it would have Dx and Dy novanishing and only a horizontal force on the x axis, which produces a pair acting on that member BD.