zr95
- 25
- 1
Homework Statement
Homework Equations
Series: Req = r1 + r2...
Parallel: 1/req = 1/r1 + 1/r2...
The Attempt at a Solution
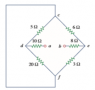
This is my professors solution for the problem and of course without any explanation it doesn't make sense to me. Under what principle can he justify immediately adding 10 + 8?
For my solution I redrew the circuit and did:
5||20 = 4
10+4 = 14
3 || 6 = 2
2+8 = 10
10+14 = 24
Another question: Had I not redrawn the circuit I still would've gotten 14 and 10 but I would've thought they would be in parallel with each other with the way its drawn out?
I understand redrawing it is the easiest way to make sure I have it correct but there won't be enough time unless I immediately recognize what it looks like.