Finding Shear Stress at Point E on a Beam

[aaronfue]

Homework Statement

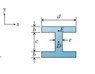
Determine the shear stress, \tau_E, at point E that corresponds to the maximum shear force along the length of the beam. V = 25kN

b= 55 mm
c=150 mm
d=110 mm
e=65 mm

Homework Equations

\tau_E = \frac{V*Q}{I*t}

Q = \bar{y}'*A'

The Attempt at a Solution

I was able to find the shear stress for point D, but I'm having trouble finding point E. How do I find Q for that point? I read an example in my textbook but there was not much of an explanation.

Is point E the centroid for the area when the neutral axis is at point D? If this is the case, I would be able to find the shear stress.

 

[SteamKing]

Unfortunately, the diagram is not clear on where point E is located. The shear stress in the beam takes a large jump at the intersection of the upper flange and the web of the beam. In any case, Q will be the first moment of the area between E and the top of the flange, referenced about the neutral axis.

 

[nvn]

Is point E the centroid for the area when the neutral axis is at point D?

I am not sure, since I did not try it.

Technically speaking, we could say point E is located at a distance 0.80*b from the top edge of the upper flange. I.e., point E is located at (0.50*c + 0.20*b) from point D. Therefore, based on this assumption, you could find the shear stress at point E.

 

[aaronfue]

I am not sure, since I did not try it.

Technically speaking, we could say point E is located at a distance 0.80*b from the top edge of the upper flange. I.e., point E is located at (0.50*c + 0.20*b) from point D. Therefore, based on this assumption, you could find the shear stress at point E.

Thanks for all of the input. I was told to assume that point E was located at the point where the web meets the flange. Great drawing!(sarcasm) Got this one wrong.

 

[pongo38]

Glad you are sorted now. However, shear stress is not evaluated at a point, but at a section. There is a difference.