SUMMARY
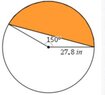
The discussion focuses on calculating the area of a shaded region formed by a circular sector and an isosceles triangle. The area of the shaded region, denoted as \(A\), is determined using the formula \(A = A_S - A_T\), where \(A_S = \frac{1}{2}r^2\theta\) represents the area of the circular sector and \(A_T = \frac{1}{2}r^2\sin(\theta)\) represents the area of the isosceles triangle. The specific values used in the calculations are \(r = 27.8\) inches and \(\theta = \frac{5}{6}\pi\) radians, resulting in a shaded area of approximately \(818.4\) square inches.
PREREQUISITES
- Understanding of circular geometry and sectors
- Knowledge of trigonometric functions, specifically sine
- Familiarity with radians and degree conversions
- Basic algebra for manipulating area formulas
NEXT STEPS
- Study the properties of circular sectors and their applications
- Learn about trigonometric identities and their uses in geometry
- Explore the conversion between degrees and radians
- Practice solving area problems involving composite shapes
USEFUL FOR
Students in geometry, educators teaching area calculations, and anyone interested in applying trigonometry to solve real-world problems involving circular and triangular shapes.