SUMMARY
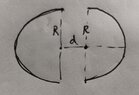
The discussion centers on calculating the capacitance of two adjacent hemispheres with radius R and distance d, each charged with ±Q. The participants highlight that the assumption of uniformly distributed charge does not yield equipotential hemispheres, complicating capacitance calculations. It is established that these hemispheres cannot be treated as standard conductors, which further complicates the definition and calculation of capacitance in this scenario. The lack of existing literature, such as Smythe's work, on this specific case indicates a gap in the theoretical framework.
PREREQUISITES
- Understanding of electrostatics and capacitance principles.
- Familiarity with the concept of electric fields and charge distribution.
- Knowledge of equipotential surfaces and their significance in electrostatics.
- Basic grasp of mathematical modeling in physics.
NEXT STEPS
- Research the mathematical modeling of capacitance for non-standard geometries.
- Study the implications of charge distribution on electric fields in electrostatics.
- Explore advanced texts on electrostatics, particularly Smythe's work on capacitance.
- Investigate numerical methods for solving complex electrostatic problems.
USEFUL FOR
This discussion is beneficial for physicists, electrical engineers, and students studying electrostatics, particularly those interested in advanced capacitance calculations and electric field theory.