Capacitance varying with temperature.

[Jonnyto]

Homework Statement

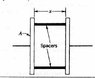
A capacitor is to be designed to operate, with constant capacitance, in an environment of fluctuating temperature. As shown in Fig. 23, the capacitor is a parallel-plate type with plastic "spacers" to keep the plates aligned. (a) Show that the rate of change of capacitance C with temperature T is given by

dC/dT= C[dA/AdT - dx/xdt]

where A is the plate area and x the plate separation. (b) If the plates are aluminum, what should be the coefficient of thermal expansion of the spacers in order that the capacitance not vary with temperature? (Ignore the effect of the spacers on the capacitance)

Homework Equations

C=Q/V C=εA/d

The Attempt at a Solution

I have no idea how to approach the problem. So far I can only tell that the temperature is causing the area change and I'm assuming that it's also causing the plates to move away or towards each other.

 

[Sunil Simha]

It is known that C=ε_0\frac{A}{d} right? Now differentiate this with respect to temperature (using chain rule to obtain the required result; If you have not learned chain rule yet, go through your maths textbook. I'm sure you'll get it there.)

Assuming that the plates are ultra-thin (i.e. they have negligible thickness) x doesn't change with temperature. So, the spacers should simply prevent A from changing.

P.S. Could you please upload the diagram ( a rough sketch is fine). I'm not able to visualize the spacers.

 

[Jonnyto]

Okay I have attached the diagrams. How would I go about differentiating with respect to Capacitance and Temperature.

 

[Sunil Simha]

Okay I have attached the diagrams. How would I go about differentiating with respect to Capacitance and Temperature.

Just so the I can answer to your queries better, have you learned about product rule, quotient rule and chain rule in differentiation?

 

[Jonnyto]

Yes I have.

 

[Sunil Simha]

In that case you need to differentiate ε₀A/x w.r.t. T. Use chain rule and quotient rule here.

For the capacitance to not change with temperature, the expression for dC/dT should be equated to zero (because capacitance should remain constant according to your question).

Thus you can obtain a relation between the infinitesimal change in area w.r.t. T (dA/dT) and the infinitesimal change in x with respect to temperature(dx/dt). You can find dA/Adt using tables (that is simply the coefficient of thermal expansion of area). Thus you can find dx/xdT.

Edit: dx/xdT is the coefficient of linear expansion of the plastic.

 

[Jonnyto]

In that case you need to differentiate ε₀A/x w.r.t. T. Use chain rule and quotient rule here.

For the capacitance to not change with temperature, the expression for dC/dT should be equated to zero (because capacitance should remain constant according to your question).

Thus you can obtain a relation between the infinitesimal change in area w.r.t. T (dA/dT) and the infinitesimal change in x with respect to temperature(dx/dt). You can find dA/Adt using tables (that is simply the coefficient of thermal expansion of area). Thus you can find dx/xdT.

Edit: dx/xdT is the coefficient of linear expansion of the plastic.

Ahh! Thank you so much! I had no idea about the linear expansion.