- #1
penguinnnnnx5
- 36
- 0
Homework Statement
A 1.4 kg object at x = 2.00 m, y = 3.10 m moves at 4.9 m/s at an angle 45° north of east. Calculate the magnitude of the object's angular momentum about the origin.
Answer is 5.3 kg m^2 /s
Homework Equations
These were the only three I could think of:
L=Iω
L=mvr
ω=v/r
The Attempt at a Solution
First attempt:
L=mvr
L= (1.4)(4.9)sqrt(4+3.1^2)
L=25.3077, not the right answer
Second attempt:
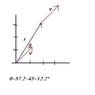
Diagram here.
I tried to find the tangential velocity as shown:
∠2 = arctan (3.10/2.00) = 57.17°
Vtan = 4.9cos(45) / cos(57.17) = 6.390914 m/s
ω=v/r=6.390914/Sqrt(4+3.1^2) = 1.73234 rad/s
Then I'm not really sure how to proceed after this because I'm not entirely sure what equation to use for I.
Third attempt:
Vtan=v ∴
L=1.4(6.390914)(sqrt(4+3.1^2) = 8.94728 m/s, not the right answer
Is my diagram wrong or am I missing something very important?
Last edited: