Finding the max angle of a longboard deck before the wheels slip

[CK_KoopaTroopa]

Hi, I'm making an electric longboard and trying to write an app for my phone to function as the remote. I've got a bunch of fancy Star-Trek-esque indicators on it, one of which is the pitch and roll of the deck. All the indicators have "danger zones" and turn red when they hit them, and for this the danger zone will be dynamic as your speed changes so I'm trying to find the maximum angle (roll) in degrees that the board can be tilted to turn before the wheels slip on the road based on speed. I thought I had it down, but must have done something wrong because the results don't quite make sense so here's my process (sorry for the picture being so scatter-brained haha)

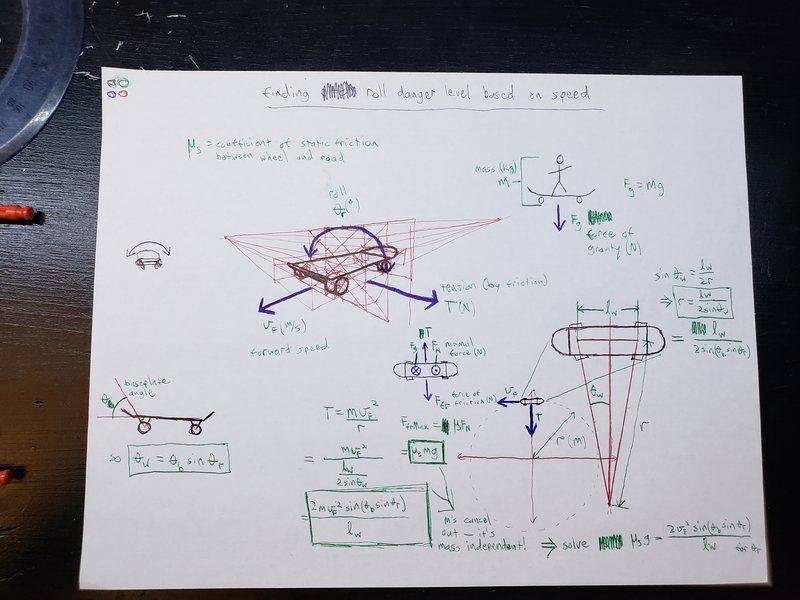
So, the board turns in a circle whose radius r changes as some function of the roll, θ_r. More directly, the radius depends on the angle of the wheels with the midline of the deck, θ_w (see lower right section of picture for clarification). One can calculate this correlation based on the length between the trucks, l_w by using SOH (sin = opposite/adjacent) to get
sinθ_w = l_w / 2r ⇒ r = l_w/2sinθ_w
To get θ_w as a function of θ_r, I figured out it's a sinusoidal relationship to the baseplate angle θ_b, specifically
θ_w = θ_bsinθ_r
Therefore, the radius of the curve is
r = l_w / 2sin(θ_bsinθ_r).

Now, to get the centrifugal force, the formula is mv² / r, so we can simply plug in what we got for r to get
F_cen = mv² / (l_w / 2sin(θ_bsinθ_r))
which can simplify to
F_cen = 2mv²sin(θ_bsinθ_r) / l_w

The force that has to counteract that is the force of friction between the wheels and the road (with axis of movement parallel to wheel's axis of rotation), the maximum of which is F_fric = μmg. Therefore to figure out the maximum θ_r (the end goal of all this), we need to
solve F_fric = F_cen for θ_r

Oh boy, here we go.
μmg = 2mv²sin(θ_bsinθ_r) / l_w
First of all, the m's cancel out, meaning it's apparently mass independent (makes sense; a heavier person will produce more centrifugal force but also push harder on the ground increasing friction), so now let's just algebra the crap outta this:
μgl_w = 2v²sin(θ_bsinθ_r)
μgl_w / 2v² = sin(θ_bsinθ_r)
sin^-1(μgl_w / 2v²) = θ_bsinθ_r
sin^-1(μgl_w / 2v²) / θ_b = sinθ_r
sin^-1(sin^-1(μgl_w / 2v²) / θ_b) = θ_r
Therefore,
θ_rMax = sin^-1(sin^-1(μgl_w / 2v²) / θ_b)

This should be the end of the problem, but when I applied it to the program and plugged in appropriate values for all the variables, it wasn't behaving properly (for example, when the coefficient of friction is set to 1 the maximum roll should be 90 regardless of speed but it still changes as the speed changes). Any ideas on what I might've done wrong? Do I need to bring calculus into this somewhere as an optimization problem? I'm at a loss...

 

[Bystander]

Are the wheels "crowned?" Any cylinder/roller/wheel with a non-zero width is going to be slipping all the time in a turn.

 

[CK_KoopaTroopa]

Are the wheels "crowned?" Any cylinder/roller/wheel with a non-zero width is going to be slipping all the time in a turn.

I don't think they're crowned if I understand that term correctly... I haven't actually purchased or built anything yet, I'm just getting the software down first and will put in values later. I realize that the wheels are slipping during a turn due to the geometry of how it works and therefore the curve itself can't be perfectly measured with this method, but I'm only trying to calculate the point at which it will cross from that required direct slippage into centrifugal force induced skidding. Maybe I am going about this entirely the wrong way though... Is there a better approach...?

 

[A.T.]

when the coefficient of friction is set to 1 the maximum roll should be 90 regardless of speed

Why?

 

[CK_KoopaTroopa]

Why?

Might be missing something here, but if the coefficient of friction is 1, doesn't that mean the surfaces have infinite friction between them (cannot move no matter how much force is applied)? And if that's the case, the maximum amount you could tilt the board to steer should be the maximum amount possible in its range of motion, which theoretically is 90°. In practice it would be less than that due to collisions, but mathematically speaking the maximum roll relative to exactly flat is exactly sideways.

 

[A.T.]

Might be missing something here, but if the coefficient of friction is 1, doesn't that mean the surfaces have infinite friction between them (cannot move no matter how much force is applied)?

No.

 

[CK_KoopaTroopa]

Ok... Care to elaborate? What DOES a coefficient of 1 mean?

 

[A.T.]

What DOES a coefficient of 1 mean?

Why don't you look at your own post:

... maximum of which is F_fric = μmg ...

What does μ = 1 imply?

 

[CK_KoopaTroopa]

Ohhhkay. I'm not sure what algorithm I was confusing with this but that makes more sense. Also, having thought about this for a couple days I'm realizing that it wouldn't work anyway, because it doesn't account for tilted roadways etc. Better to measure acceleration of the board directly which would be more reliable anyway since I can directly compare that with μmg.

As for the constant wheel slippage during a turn, maybe I could do some research and measurements and come up with a formula for a dynamic coefficient of friction for the wheels based on speed and maybe vibration, which would be more accurate.