Finding the minimum and maximum distances using Lagrange Multipliers

[theBEAST]

Homework Statement

What I don't understand is why you can maximize the distances squared - d². Isn't d² different from d? I don't see how they can get you the same value.

 

[Ray Vickson]

Homework Statement

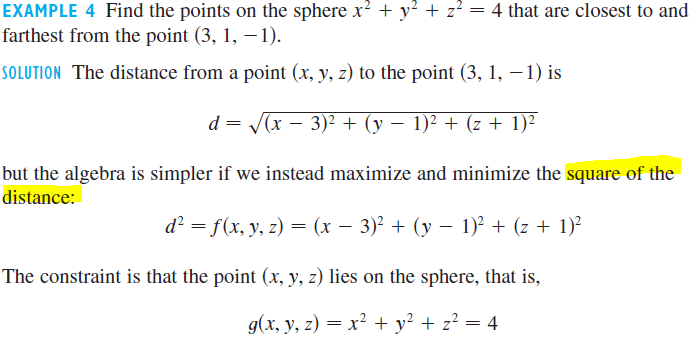
What I don't understand is why you can maximize the distances squared - d². Isn't d² different from d? I don't see how they can get you the same value.

They don't have the same values (unless they happen to be 0 or 1), but they are maximized or minimized at the same points (x,y,z). Think about it: how could it be otherwise?

RGV

 

[HallsofIvy]

Letting distance be "D", so we can distinguish it from the differential, "d", d(D^2)/dt= 2D (dD/dt)= 0. If D itself is not 0, d(D^2)/dt will be 0 if and only if dD/dt is 0.

 

[Ray Vickson]

They don't have the same values (unless they happen to be 0 or 1), but they are maximized or minimized at the same points (x,y,z). Think about it: how could it be otherwise?

RGV

As HallsofIvy has pointed out, the stationary points are the same in both problems. However, if the original f can take both negative and positive values, a min in the squared problem can be a saddle point in the original problem (eg: f(x) = x^3 has a saddle point at x = 0 but g(x) = f(x)^2 = x^6 has a global minimum at x = 0) and a min in the original problem can be a max in the squared problem, etc. None of these issues arise if the original f is >= 0, as it is in the distance problem you cite.

RGV