bcjochim07
- 366
- 0
Phase constant --Please help me!
What is the phase constant?
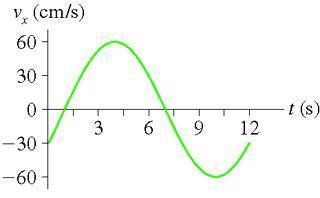
The picture didn't come yet but here's a description:
It is a velocity vs. time graph. It is sinusoidal with a period of 12 s and a max velocity of 60 cm/s. The inital value for velocity at t=0 is -30 cm/s and the value for velocity at t=12 is -30 cm/s
First I found A vmax= 2pi*A/T
60= 2pi*A/12 A=114.6
ok so I tried vo= -omega*A sin(phase constant)
omega= 2pi/T 2 pi/ 12 = pi/6
-30 cm/s = -(pi/6)*114.6 sin(phase constant)
I found phase constant = .5235 rad, but that's not right
I know that there is another angle that has the sine value, but how do I know which one is the phase constant
Homework Statement
What is the phase constant?
The picture didn't come yet but here's a description:
It is a velocity vs. time graph. It is sinusoidal with a period of 12 s and a max velocity of 60 cm/s. The inital value for velocity at t=0 is -30 cm/s and the value for velocity at t=12 is -30 cm/s
Homework Equations
The Attempt at a Solution
First I found A vmax= 2pi*A/T
60= 2pi*A/12 A=114.6
ok so I tried vo= -omega*A sin(phase constant)
omega= 2pi/T 2 pi/ 12 = pi/6
-30 cm/s = -(pi/6)*114.6 sin(phase constant)
I found phase constant = .5235 rad, but that's not right
I know that there is another angle that has the sine value, but how do I know which one is the phase constant