Finding the Resultant Amplitude & Phase: A Practice Problem

[mmmboh]

Hi, this isn't homework but a practice problem.
A particle is simultaneously subjected to three simple harmonic motions, all of the same frequency and in the x direction. The amplitudes are 0.25, 0.20, 0.15, and the face difference between the first and second is 45⁰ and between the second and third is 30⁰. Find the amplitude of the resultant displacement and its phase relative to the first component.

I made a diagram

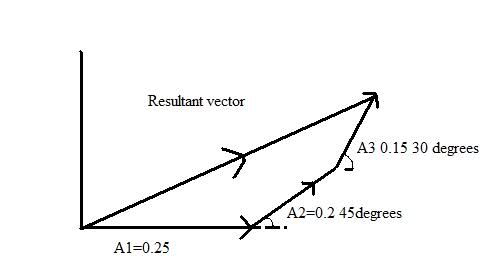
The 0.25, 0.20, and 0.15 components are represented by Z₁=A₁e^jwt, Z₂=A₂e^j(wt+a), and Z₃=A₃e^j(wt+b), adding them all together to give me the resultant component, and simplifying gives me: Z=e^jwt[A₁+A₂e^ja+A₃e^jb]...so what I would think I am suppose to do is find the x component of the resultant vector and the y component, and use Pythagorean to find the resultant vector and then do arctan(y/x) to get the phase angle. The answers are 0.52 and 33.5⁰.
I can get 0.52 for the amplitude, but that is only by taking the x component of the resultant vector and ignoring the rest, if I do it with Pythagorean I get [0.52² +0.216²]^1/2=0.56, and the angle is arctan (0.216/0.52)=22.5...so apparently I am wrong, can someone help please?

 

[willem2]

I can get 0.52 for the amplitude, but that is only by taking the x component of the resultant vector and ignoring the rest, if I do it with Pythagorean I get [0.52² +0.216²]^1/2=0.56, and the angle is arctan (0.216/0.52)=22.5...so apparently I am wrong, can someone help please?

I can only get 0.52 for the amplitude if I use both the x and the y component of the resultant vector. I also don't get 0.216 for the y component. If you want to know
what's wrong show your calculation

 

[mmmboh]

Ok well for the x component I did 0.25+0.20cos45+0.15cos30=0.52...and for the y component I did 0.20sin45+0.15sin30=0.216...what am I doing wrong?

 

[mmmboh]

Hm I guess if i use 75 degrees for the third one instead of 30 degrees it works, that's how I originally did it, but in the book they made it seem like that's not the way :S

Edit: I think I see my mistake