SUMMARY
The discussion focuses on finding the complex roots z1 and z2 of the equation z^2 = 1 - 2√2 i. Participants suggest using the polar form of complex numbers and De Moivre's formula for simplification. It is established that while polar form can be used, expressing z as a + bi and solving for real components is more straightforward. The roots are identified as not being conjugate pairs but rather negatives of each other, with the solution involving solving a system of equations for real numbers a and b.
PREREQUISITES
- Understanding of complex numbers in the form z = a + bi
- Familiarity with polar form of complex numbers
- Knowledge of De Moivre's formula
- Ability to solve systems of equations
NEXT STEPS
- Learn how to express complex numbers in polar form
- Study De Moivre's formula and its applications in finding roots of complex numbers
- Practice solving systems of equations involving real and imaginary parts
- Explore numerical methods for calculating n-th roots of complex numbers
USEFUL FOR
Students studying complex analysis, mathematicians working with complex equations, and anyone interested in mastering the roots of complex numbers.
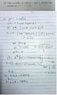
![DSC_0014~4[1].jpg](/data/attachments/53/53982-2ad9497cc3b07f69372b1b959bc46ed5.jpg?hash=KtlJfMOwf2)