- #1
kelvin macks
- 60
- 0
Homework Statement
in order to get z1 and z2 , i tried to express z^2 into polar form, but z is to the power of 2, I'm not sure whether it can be epressed in polar form of not. by the way , here's my working. how should i proceed? i don't think my ans is correct.
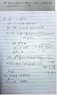
![DSC_0014~4[1].jpg](/data/attachments/53/53982-2ad9497cc3b07f69372b1b959bc46ed5.jpg)