Fluid Dynamic Torque [in symbols]

[Bluestribute]

Homework Statement

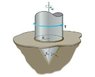
The conical bearing is placed in a lubricating Newtonian fluid having a viscosity μ.
Determine the torque T required to rotate the bearing with a constant angular velocity of ω. Assume the velocity profile along the thickness t of the fluid is linear.

Homework Equations

v=ωr
τ=μ(dy/dt)

The Attempt at a Solution

So our professor was in the middle of a problem like this before running out of time and abandoning it . . . so I'm not really sure where to start. I know trig is used to find a relationship between R and H, but setting up the integral and actually integrating . . . I'm lost . . .

 

[Chestermiller]

Let z represent the distance measured upward from the vertex of the cone. What is the radius at location z in terms of θ? What is the relative velocity between the cone and the stator surface at location z? If the spacing in the figure is t, what is the horizontal spacing between the cone surface and the stator surface in terms of θ? What is the shear rate at location z?

Chet

 

[Bluestribute]

r=ztanθ

Isn't velocity ωr? So ωztanθ?

I don't really understand that last points you made, but so far is this correct? I know the final answer has a sinθ in it, and it's because the thickness of the cone is used instead of height. But the reasoning behind the confuses me too . . .

 

[Chestermiller]

r=ztanθ

Isn't velocity ωr? So ωztanθ?

I don't really understand that last points you made, but so far is this correct?

Yes.

I know the final answer has a sinθ in it, and it's because the thickness of the cone is used instead of height. But the reasoning behind the confuses me too . . .

The horizontal spacing between the cone and the stator is t/cosθ=tsecθ, so the shear rate is:
$$δ=z\frac{ω\tanθ}{t\secθ}=z\frac{ω\sinθ}{t}$$
What is the shear stress τ(z)?
What is the torque on the increment of cone surface between z and z + dz?

Chet

 

[Chestermiller]

Incidentally, this can be done more precisely if we use spherical coordinates.

Chet