Aerospace
- 39
- 0
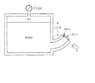
The closed vessel contains water with an air pressure of 10 psi at the water surface. One side of the vessel contains a spout closed by a 6-inch diameter circular gate hinged along one side. Horizontal axis of the hinge is located 10 ft below the water surface. Determine the minimum torque that needs to be applied at the hinge to hold the gate shut.
Okay.
Here's what I am thinking, and please let me know if I am doing this correctly.
First, I'm trying to find the resultant Force = F. Here's where I am slightly confused. Do I take this body as a curved surface or not? because the gate is located at a spout which is circular. If not, then what I did was just
A = pi * r^2 = 9*pi in^2 = pi/16 ft^2
hc (vertical distance from fluid surface to centroid of area) = 10 ft
specific weight = 62.4 lb/ft^3
F = sp wt * hc * A = 122.52 lb
Torque (T) = F * radius = F * (3/12)ft = 30.63 lb-ft
Is that right?
Okay.
Here's what I am thinking, and please let me know if I am doing this correctly.
First, I'm trying to find the resultant Force = F. Here's where I am slightly confused. Do I take this body as a curved surface or not? because the gate is located at a spout which is circular. If not, then what I did was just
A = pi * r^2 = 9*pi in^2 = pi/16 ft^2
hc (vertical distance from fluid surface to centroid of area) = 10 ft
specific weight = 62.4 lb/ft^3
F = sp wt * hc * A = 122.52 lb
Torque (T) = F * radius = F * (3/12)ft = 30.63 lb-ft
Is that right?