Force components acting on an airfoil

[FEAnalyst]

TL;DR

Are these formulas for lift and drag correct ?

Hi,

I have a simple question but I want to be 100% sure that my reasoning is correct. Take a look at this picture showing forces acting on an airfoil:

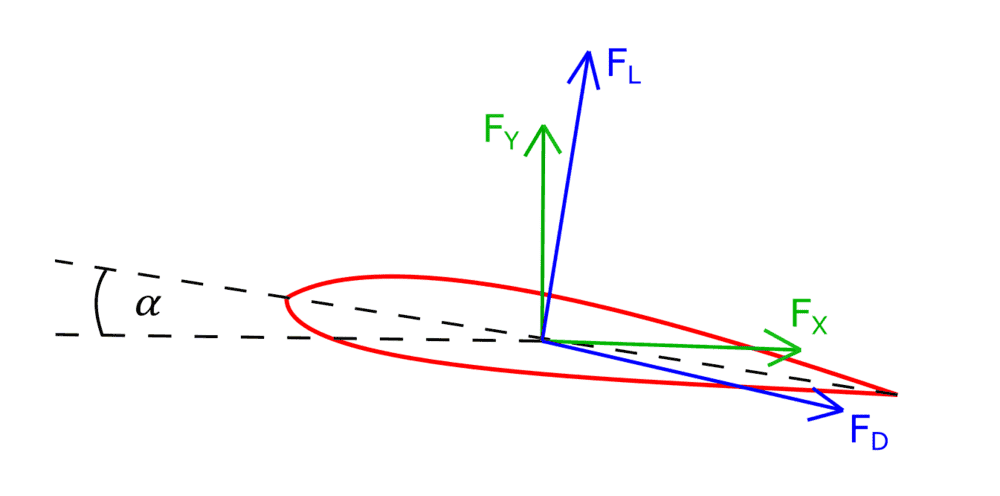
Green forces (X and Y components) are known from CFD software but I need the values of blue components (lift and drag). Of course for zero angle of attack they will be equal to each other but I need formulas for nonzero angle. In the literature I've found the following equation for lift: $$F_{L}=F_{X} \sin{\alpha} - F_{Y} \cos{\alpha}$$ From this I figured out the formula for drag: $$F_{D}=F_{X} \cos{\alpha} + F_{Y} \sin{\alpha}$$ Are these equations correct ? If not then how they should look like ?

Thanks in advance for your help

 

[trurle]

Y axis should be inverted in diagram above for equation you provide to be correct.

 

[FactChecker]

It's always the part that one is most confident about that turns out to be wrong. So be careful of any "of course" statements. :>)

 

[FEAnalyst]

Thanks for reply. Is the first formula (for lift) correct and second one (for drag) wrong ? Could you tell me what should be changed ? Only sign so that it becomes $F_{D}=F_{X} \cos{\alpha}- F_{Y} \sin{\alpha}$ ?

 

[FactChecker]

Either change your diagram or change every sign of $F_Y$ in your equations.

PS. Always test the cases of $\alpha=0$ and $\alpha=90$ to make sure that your sign convention is correct.

 

[FEAnalyst]

So, just to make sure, for the diagram I attached to my first post the correct formulas are: $F_{L}=F_{X} \sin{\alpha}+ F_{Y} \cos{\alpha}$ and $F_{D}=F_{X} \cos{\alpha}- F_{Y} \sin{\alpha}$, right ?

 

[FactChecker]

Looks good to me.

 

[FEAnalyst]

Thank you very much. Apparently there was an error in the article where I’ve found the first formula which confused me and I couldn’t figure out how to derive it.

 

[FactChecker]

Thank you very much. Apparently there was an error in the article where I’ve found the first formula which confused me and I couldn’t figure out how to derive it.

Any time you get such an equation from a different source, the chances are good that they do not use the same coordinates and sign convention. So you must make the appropriate conversions.

 

[David Lewis]

The vectors should be drawn to scale. That will make things easier to visualize and allow you to check your work.

 

[tech99]

My understanding is that, irrespective of the shape or angle of attack of the wing, lift is a force at right angles to the wind and drag is a force in line with the wind. That is different to the diagram.

 

[FEAnalyst]

My understanding is that, irrespective of the shape or angle of attack of the wing, lift is a force at right angles to the wind and drag is a force in line with the wind. That is different to the diagram.

That's interesting aspect. Some diagrams show lift and drag as always vertical and horizontal, irrespective of the angle of attack (like green vectors on my drawing). But others show these forces as parallel and perpendicular to chord line (like blue vectors on my drawing). For example:

https://www.grc.nasa.gov/www/k-12/airplane/climb.html

The definition of drag is force acting opposite to velocity vector which follows chord line changing for different angles of attack. This would suggest that the second way of representing forces acting on airfoil is correct. Lift definition is less clear in this sense. On the other hand it seems that most diagrams follow the first approach. Thus I'm confused which way is correct.

 

[FactChecker]

That's interesting aspect. Some diagrams show lift and drag as always vertical and horizontal, irrespective of the angle of attack (like green vectors on my drawing). But others show these forces as parallel and perpendicular to chord line (like blue vectors on my drawing). For example:

https://www.grc.nasa.gov/www/k-12/airplane/climb.html

The definition of drag is force acting opposite to velocity vector which follows chord line changing for different angles of attack. This would suggest that the second way of representing forces acting on airfoil is correct. Lift definition is less clear in this sense. On the other hand it seems that most diagrams follow the first approach. Thus I'm confused which way is correct.

The NASA diagram is of a plane in a climb, so the actual direction of motion is not horizontal. In the text, they define lift and drag as "aerodynamic forces relative to the flight path".

One must be aware that different axis systems may be used and preferred by different specialists. Stability and control people like the wind axis. Others may prefer the body axis. Appropriate conversions are necessary. That being said, the term "lift" should probably be reserved only for the wind axis while something like $-F_z$ used to denote upward force in the body axis (z is often positive down).

 

[tech99]

It seems to me more logical to refer lift and drag to the wind direction. The "aerofoil" might not be a wing - it could be an irregular object such as a building, or a golf ball, where we have no chord to refer to.
If we refer to the chord of the wing, it becomes difficult when the aeroplane has sink and glide angle.
Further, it is messy if lift and drag are not at right angles and if lift is not in line with weight.
I have found that for sailing vessels, where we do not have a simple aerofoil, to refer everything to the wind makes the understanding so much easier, and allows simpe explanation of leeway (equivalent to glide angle for an aeroplane).

 

[FactChecker]

It seems to me more logical to refer lift and drag to the wind direction. The "aerofoil" might not be a wing - it could be an irregular object such as a building, or a golf ball, where we have no chord to refer to.

Eventually, one is usually interested in the forces in terms of other coordinates anyway. So conversions are necessary.

If we refer to the chord of the wing, it becomes difficult when the aeroplane has sink and glide angle.
Further, it is messy if lift and drag are not at right angles and if lift is not in line with weight.

If there is a sink rate, then the wind axis does not line up with the Earth axis anyway and lift is not in line with weight. The same can be said if there is any roll angle.
That being said, the wind axis is as good as any and better (i.e. more convenient) for aerodynamics and wind tunnel work.