How can I solve the Spring Balance problem using alternative methods?

[cwill53]

Homework Statement

The rings A, B, C of three spring-balances are fixed to the horizontal board as shown in the Figure. A cord is attached to the hook of each balance and the free ends of the cords are tied together in a knot D. The readings of the balances are 8lbs; 7lbs, 13lbs. Determine the angles $\alpha$ and $\beta$ between the directions of the cords.

Ans. $\alpha$ = 27 $^{{\circ}}$48’
$\beta$=32$^{{\circ}}$12’

Relevant Equations

$$\sum \vec{F}=m\vec{a}$$

Here is the diagram:

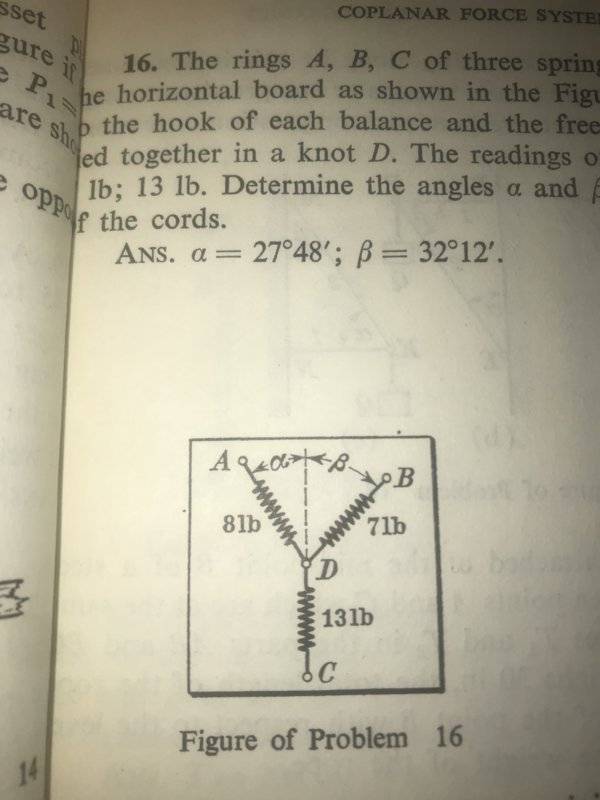
I’ve only drawn the diagram and made equations for the sum of forces in the x-directions and y-directions:
$\sum F_{x}=(7 lbs)sin\beta+(8 lbs)sin\alpha=0$
$\sum F_{y}=(8 lbs)cos\alpha+(7 lbs)cos\beta-13 lbs=0$

 

[BvU]

Hi,

So you have two equations with two unknowns. What stops you from solving ?

https://www.physicsforums.com/threads/homework-help-guidelines-for-students-and-helpers.686781/

 

[archaic]

If you solve for one of the sines in the first equation, would you be able to use $\cos x=\sqrt{1-\sin^2x}$?

 

[cwill53]

Hi,

So you have two equations with two unknowns. What stops you from solving ?

https://www.physicsforums.com/threads/homework-help-guidelines-for-students-and-helpers.686781/

I still don't see how to do this. Two equations two unknowns. I get that. But I'm having trouble solving it.

 

[archaic]

I still don't see how to do this. Two equations two unknowns. I get that. But I'm having trouble solving it.

$$7\sin\beta+8\sin\alpha=0\Leftrightarrow\sin\beta=-\frac 87\sin\alpha\\\cos\beta=\sqrt{1-\sin^2\beta}$$

 

[BvU]

But I'm having trouble solving it.

Have you learned how approach solving $a\sin\theta + b\cos\theta = c$ ?

 

[cwill53]

Have you learned how approach solving $a\sin\theta + b\cos\theta = c$ ?

I probably have, but it's not coming to me even after a long time of thinking about it. My trig identities suck.

After reading what etothepi said, whose post appears to be removed, I got

$$(64 lbs^{2})(cos^{2}\alpha +sin^{2}\alpha )+(49lbs^{2})(cos^{2}\beta +sin^{2}\beta)=169lbs^{2}$$

 

[etotheipi]

I probably have, but it's not coming to me even after a long time of thinking about it. My trig identities suck.

After reading what etothepi said, whose post appears to be removed, I got

$$(64 lbs^{2})(cos^{2}\alpha +sin^{2}\alpha )+(49lbs^{2})(cos^{2}\beta +sin^{2}\beta)=169lbs^{2}$$

Don't forget the cross terms!

I removed it because I don't think it actually gets you anywhere helpful even if you apply the $\cos{(\alpha - \beta)}$ identity. @archaic's suggestion gets you the right answer.

 

[cwill53]

Don't forget the cross terms!

I removed it because I don't think it actually gets you anywhere helpful even if you apply the $\cos{(\alpha - \beta)}$ identity. @archaic's suggestion gets you the right answer.

Sorry, I'm still not understanding how that substitution works.
I got here: $(8lbs)cos \alpha+ (7lbs)\sqrt{1+\frac{8}{7}sin\alpha }$

 

[etotheipi]

You have $\sin{\beta} = \frac{-8\sin{\alpha}}{7} \implies \cos{\beta} = \sqrt{1-\sin^2{\beta}} = \sqrt{1-\frac{64\sin^2{\alpha}}{49}}$. Now you can substitute $\cos{\beta}$ back into the second equation which gives you $$7\sqrt{1-\frac{64\sin^2{\alpha}}{49}} = 13 - 8\cos{\alpha}$$ Then you're in a position to square both sides and solve for $\alpha$. You'll need to use $\cos^{2}{\alpha} = 1-\sin^{2}{\alpha}$.

 

[cwill53]

You have $\sin{\beta} = \frac{-8\sin{\alpha}}{7} \implies \cos{\beta} = \sqrt{1-\sin^2{\beta}} = \sqrt{1-\frac{64\sin^2{\alpha}}{49}}$. Now you can substitute $\cos{\beta}$ back into the second equation which gives you $$7\sqrt{1-\frac{64\sin^2{\alpha}}{49}} = 13 - 8\cos{\alpha}$$ Then you're in a position to square both sides and solve for $\alpha$. You'll need to use $\cos^{2}{\alpha} = 1-\sin^{2}{\alpha}$.

I can't see how this yields a solution. I end up getting that alpha is 94.17 degrees which is incorrect.

$7\sqrt{1-\frac{64}{49}sin^{2}a}=13-8cos\alpha$
$7\sqrt{1-\frac{64}{49}sin^{2}a}=(13+\sqrt{1-64sin^{2}a})$
$\Rightarrow 49-64sin^{2}a=-64sin^{2}a-26\sqrt{1-64sin^{2}a}+170$

 

[etotheipi]

We square both sides of $$7\sqrt{1-\frac{64\sin^2{\alpha}}{49}} = 13 - 8\cos{\alpha}$$ to obtain $$49\left(1-\frac{64\sin^2{\alpha}}{49} \right) = 49 - 64\sin^2{\alpha} =169 - 208\cos{\alpha} + 64\cos^2{\alpha}$$ Now we substitute $\sin^{2}{\alpha}$ for $(1-\cos^{2}{\alpha})$, $$49 - 64(1-\cos^{2}{\alpha}) =169 - 208\cos{\alpha} + 64\cos^2{\alpha}$$ Hopefully you can see that the $64\cos^{2}{\alpha}$ cancels on both sides. If you simplify that you can then get $\cos{\alpha}$

 

[cwill53]

We square both sides of $$7\sqrt{1-\frac{64\sin^2{\alpha}}{49}} = 13 - 8\cos{\alpha}$$ to obtain $$49\left(1-\frac{64\sin^2{\alpha}}{49} \right) = 49 - 64\sin^2{\alpha} =169 - 208\cos{\alpha} + 64\cos^2{\alpha}$$ Now we substitute $\sin^{2}{\alpha}$ for $(1-\cos^{2}{\alpha})$, $$49 - 64(1-\cos^{2}{\alpha}) =169 - 208\cos{\alpha} + 64\cos^2{\alpha}$$ Hopefully you can see that the $64\cos^{2}{\alpha}$ cancels on both sides. If you simplify that you can then get $\cos{\alpha}$

I see, I thought I was supposed to use the substitution for cos(a) on both sides.

 

[etotheipi]

I see, I thought I was supposed to use the substitution for cos(a) on both sides.

Ah. Yes the general strategy here was to try and obtain some equation only in one of $\sin{\alpha}$, $\sin{\beta}$, $\cos{\alpha}$ or $\cos{\beta}$, because then in the worst case you can do a substitution and you get a polynomial and in the best case (like here) you don't get any higher order terms and the answer comes straight out.

 

[cwill53]

Ah. Yes the general strategy here was to try and obtain some equation only in one of $\sin{\alpha}$, $\sin{\beta}$, $\cos{\alpha}$ or $\cos{\beta}$, because then in the worst case you can do a substitution and you get a polynomial and in the best case (like here) you don't get any higher order terms and the answer comes straight out.

Thanks a lot for your patience, I finally got the answer.

 

[etotheipi]

Interestingly, the way I first proposed gives some peculiar results. Squaring both equations, $$49\sin^2{\beta} + 112\sin{\alpha}\sin{\beta} + 64\sin^{2}{\alpha} = 0$$ $$49\cos^2{\beta} + 112\cos{\alpha}\cos{\beta} + 64\cos^{2}{\alpha} = 169$$ and then adding, $$49 + 64 + 112\cos{\alpha - \beta} = 169 \implies \cos{(\alpha - \beta)} = \frac{1}{2}$$ gives that $\pm(\alpha - \beta) = 60^o$!

This doesn't hold for the correct values of $\alpha$ and $\beta$, but does work for other possible solutions like $(\alpha, \beta) = (-27.8^o, 32^o)$ or $(387^o, 327^o)$...

 

[cwill53]

Interestingly, the way I first proposed gives some peculiar results. Squaring both equations, $$49\sin^2{\beta} + 112\sin{\alpha}\sin{\beta} + 64\sin^{2}{\alpha} = 0$$ $$49\cos^2{\beta} + 112\cos{\alpha}\cos{\beta} + 64\cos^{2}{\alpha} = 169$$ and then adding, $$49 + 64 + 112\cos{\alpha - \beta} = 169 \implies \cos{(\alpha - \beta)} = \frac{1}{2}$$ gives that $\pm(\alpha - \beta) = 60^o$!

This doesn't hold for the correct values of $\alpha$ and $\beta$, but does work for other possible solutions like $(\alpha, \beta) = (-27.8^o, 32^o)$ or $(387^o, 327^o)$...

Are there other methods to approach this problem with? Or is the only way to do is using trig identities?

 

[haruspex]

Are there other methods to approach this problem with? Or is the only way to do is using trig identities?

If you draw the triangle of forces you can apply the cosine rule to get an equation involving only one trig term.