Force exerted by aircraft dive brakes- where did I go wrong?

AI Thread Summary
The discussion revolves around calculating the average force exerted by dive brakes on an aircraft during a vertical dive. The aircraft, with a mass of 5000 kg, initially dives at 500 knots and slows to 325 knots after deploying the dive brakes. The user initially calculated the required force but arrived at a value of 65.9 kN, which conflicted with the book's answer of 16.62 kN. After further analysis, it was determined that the book's answer was incorrect, and the correct approach involves applying Newton's second law accurately, leading to the conclusion that the dive brake force is indeed around 66 kN. The user expressed relief in clarifying their understanding of the problem.
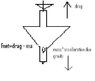
telebender
Messages
3
Reaction score
0

Homework Statement


An aircraft of 5000kg mass is diving vertically downwards at a speed of 500 knots. The pilot operates the dive brakes at a height of 10 000m and reduces the speed to 325 knots at 7000m. If the average air resistance of the remainder of the aircraft during the deceleration is 15KN what average force must be exerted by the dive brakes? (assume the engine is throttled back and is not producing any thrust)


Homework Equations



V2=u2+2as
where V= final velocity
u=original velocity
a=acceleration
s=distance

The Attempt at a Solution


First convert velocities into m/s. 1 knot=0.5145 m/s so:

u=500 knots=257.25 m/s
v=325 knots=167.21m/s

transposing above formula for a: a=(V2-u2)/2s

=-6.3696m/s2

The force causing the plane to acelerate downwards is mass*gravity (mg) so to stop the acceleration the drag force would have to be equal to mg. 5000kg * 9.81m/s2=49050N As the drag force acts opposite to acceleration call it -49050N

To acelerate the plane (in this case opposite to direction of travel) there must be an additional force of mass * aceleration (ma). 5000kg*-6.3696m/s2=-31848

The total drag force would be: (force equal to mg)+ma

-49050N+-31848N=-80898N

These figures are -ve because they are based on a negative aceleration so the actual drag force is +80898N

Take away from this the air resistance without dive brakes of 15000N=

65898N



The answer is given as 16.62KN, I have given this a lot of thought but can't work out where I've gone wrong. Any help please?
 
Physics news on Phys.org
Welcome to PF!:smile:

Don't take any shortcuts, draw a free body diagram to identify all the forces, then use Newton 2, Fnet = ma. The air resistance force is the drag force and is given. You have the weight force. Solve for the dive brake force, using Newton 2 and the correct value of the acceleration you determined (the acceleration and the net force must be in the same direction...which direction is that?).

Edit: In checking your work, you appear to have arrived at the correct answer using an unorthodox method.
 
Last edited:
Hello,
Thank you for your reply.

The answer of 16.62KN from my last post is from the book I'm working out of. The answer I arrived at was 65.9KN which is why i posted here.

https://www.physicsforums.com/attachments/35372
I have attached my attempt at a free body diagram here.

The Fnet and acceleration must be in an upwards direction as the plane is going straight down and is slowing.

From reading your reply I think I just need to multiply the mass of 5000kg by the acceleration of 6.3696m/s2 which gives 31848N. Subtracting the 15000N of air resistance gives 16.848KN. That seems quite close to the correct answer but I've somehow gained 228N

I think where I went wrong with my first attempt was that I assumed the plane was still accelerating due to gravity when the dive brakes were deployed. If this was the case would there be a force of mg reqiired to halt the acceleration in addition to the force accelerating the plane upwards as I thought?

Hope I have made my thoghts clear. Apologies if not.
thanks again
ed
 

Attachments

  • drag fbd.JPG
    drag fbd.JPG
    7.7 KB · Views: 471
What I meant is that you were right and the book was wrong.

Fnet = ma
Brake drag + other drag - mg = ma
Brake Drag + 15,000 - 5000(9.8) = 5000(6.37)
Brake Drag - 34,000 = 31,850
Brake Drag = 66,000 N

You had it right the first time...but be meticulous when using Newton's 2nd law.
 
Many thanks for your help on this Jay, I didn't even consider that the book might be wrong!
Now that's cleared up I can move on without worrying that I've misunderstood the basics.
really appreciate it,
ed
 
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »
Thread 'A cylinder connected to a hanged mass'

Thread 'A cylinder connected to a hanged mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Hot Threads

Recent Insights

Back
Top