SUMMARY
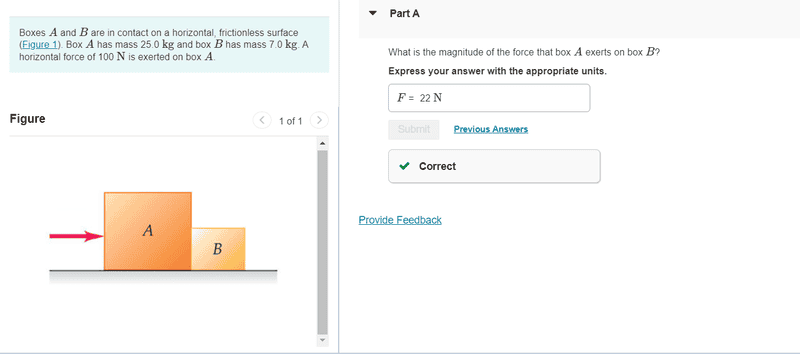
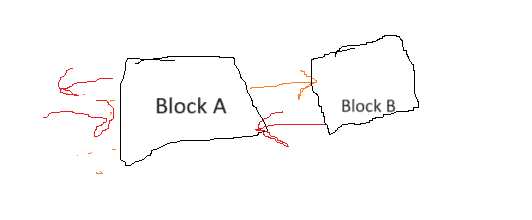
The force exerted on block B by block A when pushed on a frictionless surface is calculated using the formula mB * a, where mB represents the mass of block B and a is the acceleration. This approach is necessary because block B's inertia directly influences the force exerted by block A. In scenarios where block B is either very small or very large, the force required to maintain its acceleration alongside block A varies significantly. To analyze such problems effectively, it is essential to draw free body diagrams for each block and write the corresponding equations to clarify the forces acting on them.
PREREQUISITES
- Understanding of Newton's Second Law of Motion
- Familiarity with free body diagrams
- Knowledge of mass and acceleration concepts
- Basic principles of frictionless surfaces in physics
NEXT STEPS
- Study Newton's Second Law in detail
- Practice drawing and analyzing free body diagrams
- Explore the effects of varying mass on force calculations
- Investigate real-world applications of frictionless surfaces in physics
USEFUL FOR
Students studying physics, educators teaching mechanics, and anyone interested in understanding the dynamics of forces in multi-body systems.