SUMMARY
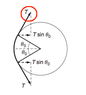
The discussion focuses on the calculation of forces acting on a pulley due to tension in a string, as presented in K&K's "Intro to Mechanics." The horizontal force from the tension is derived as ##T \sin(\theta_0)##, where ##\theta_0## is the angle made with the horizontal. Additionally, the force from the string tension is expressed as ##2T \sin(\theta)##, which results from the geometry of the system and the tangential nature of the tension forces. The analysis involves understanding the angles formed by the tension vectors and their contributions to the resultant force on the pulley.
PREREQUISITES
- Understanding of basic mechanics and vector resolution
- Familiarity with trigonometric functions and their applications in physics
- Knowledge of tension forces in pulleys and their geometric implications
- Ability to interpret diagrams and angles in mechanical systems
NEXT STEPS
- Study the geometric relationships in pulley systems using "K&K's Intro to Mechanics"
- Explore vector resolution techniques in physics problems
- Learn about the implications of tension in circular motion and its effects on forces
- Investigate the derivation of forces in different pulley configurations
USEFUL FOR
Students of physics, particularly those studying mechanics, educators teaching introductory mechanics, and anyone interested in understanding the dynamics of tension in pulley systems.