Force on a Magnet in Lenz's Law

[friendbobbiny]

Homework Statement

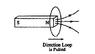
As the bar magnet (see attached diagram) leaves the loop of wire, it experiences a force opposing its exit. I understand why, according to Lenz's law, a force would oppose the bar magnet's exit. I don't understand, however, what causes the force. In this case, the force is rightwards.

In other words, what are the mechanics that cause the magnet to experience a rightwards force?

Homework Equations

See diagram.

Lenz's Law: Current is induced in a surface to oppose the change in magnetic flux through it.

The Attempt at a Solution

Here, the current induced produces a magnetic field that points in the same direction as the magnet. Hence, as the magnet tries to leave, another magnetic field somehow opposes its motion...

 

[andrevdh]

The moving magnet causes a change in magnetic flux through the coil. This induces current in the coil according to Faraday' s law of electromagnetic induction. The current in the coil now sets up a magnetic field of its own. Lenz's law helps us determine in which direction the induced current in the coil will be.

 

[Hesch]

In other words, what are the mechanics that cause the magnet to experience a rightwards force?

In short: Lenzes law says that the nature will counteract any changes in magnetic flux. So when pulling the magnet away from the loop, a current will be induced in the loop that substitutes the flux of the magnet by its own flux. All in all the amount (volume) of flux is increased.

The density of energy in a magnetic field, E_magn = ½*B*H [ J/m³]. So when magnet and loop are separated, energy must be created, to fill out the "added volume" of magnetic energy density.

F = ΔE / Δs = ( E_magn * ΔV ) / Δs = E_magn * A. ( s is distance, A is cross section area of field, V is volume of field ).

 

[andrevdh]

All that Lenz's law enables us to say is that in this case the induced current will increase the flux through the coil and thereby opposing the removal of the magnet. It is just a qualitative law not quantitative. You seem to try and evaluate the opposing force that the magnet is experiencing from the induced magnetic field.

 

[Hesch]

You seem to try and evaluate the opposing force that the magnet is experiencing from the induced magnetic field.

I'm finding the opposing force by means of energy in a magnetic field, and are not using Lenz's law to do this.

 

[andrevdh]

Don't think I can help you there, but keep in mind that it is the change in magnetic flux that brings this about. That is the induced current causes an increase in flux, not necessarily such that the total flux is kept constant. In practice one would probably measure the required force to remove the magnet and thereby calculate the induced flux change responsible for it.

 

[Hesch]

That is the induced current causes an increase in flux

The flux is not increased, the induced current in the loop will try to keep flux steady, and could do so, were the loop a superconductor. But the volume of the fluxdensity is increased, thus the energy is increased.

What is wrong with this:

F = ΔE / Δs = ( Emagn * ΔV ) / Δs = Emagn * A. ( s is distance, A is cross section area of field, V is volume of field ).

? ?

 

[andrevdh]

I would have thought that the induced current created more flux lines and thereby increased the overall energy density, but I am not at work now and can't reference my sources.

 

[andrevdh]

The induced magnetic field from the current in the coil is in the same direction as that of the magnet that is removed
from the coil. The coil thus acts as an additional magnet. It attracks the magnet as it is removed from the coil.
The source of the force is thus the coil. This effect was also used in old car speedometers - Arago's rotation effect
http://www.physics.montana.edu/demonstrations/video/5_electricityandmagnetism/demos/aragosdisc.html
https://prezi.com/dyvhcumzt6k_/electromagnetism/
The two objects become locked together and a force is required to separate them. Hope this is what you wanted to know.

 

[Hesch]

I would have thought that the induced current created more flux lines and thereby increased the overall energy density

This is wrong. The induced current in the loop will just try to keep the flux steady. It will never increase the energy density, but (here) the volume in which the steady energy density acts, thus increasing the total magnetic energy: ΔE = E_magn*Δvolume. The loop-current, creating some flux, will just substitute the disappearing flux from the magnet as it is removed. This leads to:

F = ΔE / Δs = ( E_magn * ΔV ) / Δs = E_magn * A. ( s is distance, A is cross section area of field, V is volume of field ).

I wanted to know if you agreed with that calculation?

Say that the flux were increased through the loop, a back-emf would immediately be created in the loop since emf = dψ/dt.

 

[andrevdh]

So your formula is suggesting the force is a result of a gradient created in the magnetic energy density?
The term E_magn*ΔV (have for a long time) worries me.
What does this term mean?
What would the ΔV signify?

 

[Hesch]

ΔV = change in volume.
E_magn * ΔV = ( magnetic energy density ) * Volume. In units: [ J / m³ ] * [ m³ ] ) = [ J ].

 

[andrevdh]

As you move a distance Δs along the field you go through a small volume ΔV where the field exists?

 

[Hesch]

Yes: Δs * A = ΔV. ( A = cross section area ).

 

[andrevdh]

I still would think that you need an energy gradient for a force to be present, that is the energy needs to change if
you moved a small distance in the field, that is E_magn should change.

 

[Hesch]

No, the total energy must change:

F = ΔE / Δs = ( Emagn * ΔV ) / Δs = E_magn * A.

ΔE / Δs is your gradient.

 

[andrevdh]

According to some source I can get my hands on the force is proportional to - dH²/ds
but I really don't know enought about the subject.

 

[Hesch]

E_magn = ½*B*H = ½*μ₀*H*H. Thus the force is proportional to - dH²/ds.

 

[andrevdh]

Sorry, I am not happy with what you are saying.
I would think that the force should be dependent on the change in the energy
and not just its value, that is if the energy stays constant there would be no force.

 

[Hesch]

Yes, that's what I'm saying: F = ΔE_total / Δs.

ΔE_total = 0 → F = 0

E_total is not the same as E_magn

 

[andrevdh]

Yes, but you final answer, E_magn*A, do not reflect that (I might be wrong).

 

[Hesch]

Again: What is wrong in this?

F = ΔE / Δs = ( E_magn * ΔV ) / Δs = E_magn * A. ( s is distance, A is cross section area of field, V is volume of field ).

ΔV = A * Δs.

 

[andrevdh]

Sorry, I don't know, but physically I just cannot wrap my head around what it is actually saying.
Your introduction of ΔV looks a bit artificial to me.

 

[Hesch]

Volume = (length*width)*height = basearea*height

Δvolume = basearea * Δheight

 

[andrevdh]

This ΔE/Δs asks how the energy density is changing when you move around in the space.
Your answer suggest this is how it is changing: E_magn*A ?
That does not seem sensible to me or I am just not understanding your symbols correctly.

 

[Hesch]

ΔE is the change in total energy. It could be written:

F = ΔE_total / Δs

E_total = E_magn * V, as E_magn is not an energy, but an energy density. It emerges from:

F = ΔE / Δs = ( Emagn * ΔV ) / Δs = Emagn * A. ( s is distance, A is cross section area of field, V is volume of field ).

 

[andrevdh]

Ok. Let's say we move a little distance Δs in the field.
There is a change in the amount of energy in the field equal to E₂ - E₁.
To calculate this we use the magnetic energy densities at points s₁ and s₂ : (E_m2 - E_m1 )* ΔV
where E_m is the magnetic energy per unit volume.
What does the ΔV signify? We are calculating the magnetic energy difference a little distance apart in the field. What volume, ΔV, should be used for
this calculation? Thank you for your patience with me. It usually takes me several days to understand something.

 

[Hesch]

The magnetic energy density will be about constant, as the induced current in the loop will substitute the disappearing B-field, when the magnet is gradually removed.
Thus E₂ - E₁ = E_magn * ΔV.

Of course that is not the truth when moving the magnet some 2 meters away, but nearby it's the truth.

 

[andrevdh]

We have moved a little distance Δs in the field.
The energy difference at the end and the beginning in the field is the product of the magnetic energy density and a small volume.
This product will tell us what the amount of energy is in such a small volume and not the difference in energy at the start and
end of the Δs movement.

 

[Hesch]

This product will tell us what the amount of energy is in such a small volume and not the difference in energy at the start and
end of the Δs movement.

Thus E₂ - E₁ = E_magn * ΔV.