Forced Vibration with changing amplitude

[abrandt]

Homework Statement

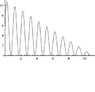
I have a damped forced vibration problem. Most problems I have dealt with have a constant amplitude sinusoidal force such as F_0sin(wt). Let's say you have an applied force that decreases each second at a constant rate over 11 seconds. It looks like this:

F=0.5*[(11-t)sin(2*pi*t)+(11-t)]; (0<= t >=11)

The graph of this force has been attached.

Homework Equations

The system is also critically damped so the system's differential equation is:

m[d^2/dt^2](x) + c(dx/dt) +kx = 0.5*[(11-t)sin(2*pi*t)+(11-t)]

The Attempt at a Solution

From here I'm not too sure how to proceed. Normally with forced vibration the solution would include both a complimentary and particlular soluntion since it is a nonhomogenous linear second order differential equation. So

x = x_c + x_p

If the force had a constant magnitude (steady state vibration) and assuming critical damping x_c would look like:

x_c=(A+B*t)e^(-W_n*t)

but since the vibration is not steady state does this equation hold true? I assume it does only because the complimentary solution is found by setting the force to zero and assuming only free vibration. A and B are then found using the initial conditions where:

A= x_c(0) or is it A=x(0)
B=Dx(0)/dt + w_n*x(0)

Then x_p needs to be found and this I am having trouble with. how would one solve this part of the differential?

 

[rude man]

A problem like this lends itself to Laplace transform technique. That means that those of us who deal in transient (and other!) problems tend to forget the classical math!

Looking back (50 years!) I see that the only rigorous way to solve this classically is via variation of parameters. Yuk.

If you will allow a moment of grandstanding - I think ALL linear, constant-coefficient diff. eq's (except for 1st order IF you can separate variables) should be solved by the Laplace transform. It reduces the diff eq to an algebraic equation and elegantly includes initial conditions and forcing functions like your oddball one. It's easy to learn; why it isn't introduced at an early stage in a diff eq course is beyond my comprehension.

I'm prepared to consider having a crack at this and getting you an answer so you could check your solution with mine. But it's a messy problem and I might give out along the way.

 

[abrandt]

i appreciate the response. i haven't covered laplace transforms much since 2nd year university and even then it dealt with simple constant amplitude periodic forces such as F_0(sin(wt)). how would i start analyzing a linearly decaying force? could you possibly point me in a direction or recommend texts that would allow me to gain a better understanding of laplace transforms dealing with time decaying forces?

 

[rude man]

Sorry, I didn't notice - you HAVE had Laplace! Makes it easy! Just transform your forcing function using tables of transforms. The fact that the input ends at t = 11 means you need the U(t-tau) transform in your forcing function.

There are very many books on the Laplace transform. My books are probably out of print but if you can obtain H H Skilling's 'Electrical Engineering Circuits' he is unbeatable as an instructor. He covers the important parts whike relating to electrical circuits, and he doesn't overdo the highfalutin stuff.

Also try Wikipedia! The price is right!

Get back with me if you have trouble.

 

[abrandt]

Thanks a lot for your help. i was able to find a website where a mathematics instructor posted their course notes on DEs and solving DEs with laplace transforms and have gained a much better understanding of laplace transforms in general. I have yet to complete a solution but it does seem like this will be a much easier method than trying to solve without.

 

[abrandt]

so I am working on a solution and i have a question about the step function. let's say that the decaying force is f(t). with u (t-11)= {0 if t< 11, 1 if t>=11}. the function of the force is then
g(t)=(1-u(t-11))* f(t)

or g(t)=f(t)-[u(t-11)*f(t)]

as i understand it. in order to do the laplace transform f(t) has to be in the form f(t-11) so:

g(t)= f(t) - u(t-11)*f(t-11+11)

from here how would i proceed. i assume that i can take the laplace of f(t) + the transform of [u(t-11)*f(t-11+11)] how would i find this second transform.

 

[rude man]

Homework Statement

I have a damped forced vibration problem. Most problems I have dealt with have a constant amplitude sinusoidal force such as F_0sin(wt). Let's say you have an applied force that decreases each second at a constant rate over 11 seconds. It looks like this:

F=0.5*[(11-t)sin(2*pi*t)+(11-t)]; (0<= t >=11)

****************************************************************
Let's start with your original problem. First, I believe you meant
f = 0.5*[(11-t)sin(2pi*t) + 11 - t], 0 <= t <= 11 , not 0 <= t >= 11.

This can be rewritten as f=0.5*[(11-t)sin(2*pi*t)+(11-t)]{U(t) - U(t-11)}

OK, now transforming this forcing function one term at a time, you'll need:

General: f(t) <--> F(s) (I always use lower case for the time function and upper case for the transformed function)

sin(wt) <--> w/(s^2 + w^2) (for you, w = 2pi*f = 2pi*1 Hz)
c <--> c/s , c = constant = 11 for you
t <--> 1/s^2
tsin(wt) <--> 2ws/(s^2 + w^2)^2
EDITED LINE: f(t)*U(t-T) <--> L[f(t+T)]exp(-sT). In your case, T = 11.
And don't forget the 0.5 factor over everything.

 

[abrandt]

Thanks a lot for your help. It turns out my force function was wrong. It is actually
F=(t-11)sin^2(pi*t)(U(t)-U(t-11))
I understand how to solve using laplace now, thanks to you, but this problem started to get quite messy quickly so i ended up solving using a math simulation software to avoid any mistakes. This is an engineering problem I'm working on at university for an industry client.
Thanks for your help.

 

[rude man]

Turned out I had to review this math myself so I got something out of it too! You were smart to use simulation software since it was for a client. But someday you might have to do it analytically!

 

[abrandt]

Not sure if your interested but after running it through Maple (math software) we got both a numerical and analytical model. The analytical model had to be solved using laplace and it ended up being over 6000 characters (this is with the new force function). This turned out to be quite the differential equation.

 

[rude man]

Very good. Tough problem on paper -challenging but also edifying. Modern math software is truly remarkable.