- #1
syavian1019
- 6
- 0
The two forces F1 and F2 act on a 27.0-kg object on a frictionless tabletop. If F1=10.2 N and F2=16.0 N find the net force on the object and its acceleration for cases (a) and (b).
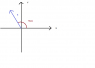
(a) is 90 degrees, in the 3rd quadrant
(b) is 120 degrees, from the positive y-axis and moving clockwise
To calculate the angles at which the resultant forces act in this problem, please start at the positive x-axis and travel counter-clockwise.
1. The net force in figure (a) (above) is?
2. The angle from the positive x-axis at which the net force in figure (a) acts is?
3. The magnitude of the acceleration of the object in figure (a) is?
For 1, I don't know which formula I'm supposed to use. I can't find it in my textbook or anywhere else... but I think for 3 it's: a = (net force)/(mass in kg)
For 2, is this how you do it?: from the positive x-axis, move counterclockwise until you hit the angle.
Thanks for all help!
(Sorry about the broken links)
(a) is 90 degrees, in the 3rd quadrant
(b) is 120 degrees, from the positive y-axis and moving clockwise
To calculate the angles at which the resultant forces act in this problem, please start at the positive x-axis and travel counter-clockwise.
1. The net force in figure (a) (above) is?
2. The angle from the positive x-axis at which the net force in figure (a) acts is?
3. The magnitude of the acceleration of the object in figure (a) is?
-----------------
For 1, I don't know which formula I'm supposed to use. I can't find it in my textbook or anywhere else... but I think for 3 it's: a = (net force)/(mass in kg)
For 2, is this how you do it?: from the positive x-axis, move counterclockwise until you hit the angle.
Thanks for all help!
(Sorry about the broken links)
Last edited: