yesmale4
- 41
- 1
- Homework Statement
- A block is resting on a ramp as shown in the figure below. You can change the inclination angle θ by raising one end of the ramp. The block has a mass m = 7.5 kg. At the interface between the ramp and the block, the coefficient of static friction is μs = 0.40, and the coefficient of kinetic friction is μk = 0.320.
the question:
Now let's go back and consider the static situation again. Let the angle θ be the angle you calculated in the first part of this problem, θ. Assume that a horizontal (parallel to the surface of Earth) force directed to the right is applied to the block. This horizontal force [(F)\vec] has a magnitude of 40 Newtons. Calculate the force due to static friction, [(f)\vec]s for this new situation, assuming that the block does not slip. Define your coordinate system such that your answer is positive if [(f)\vec]s is directed up the plane, and negative if [(f)\vec]s is directed down the plane.
- Relevant Equations
- f=ma
hey I am really hope for some help because i don't know what I am doing wrong, the angle of the first part is 21.801.
here is my solution i would like to know what I am doing wrong
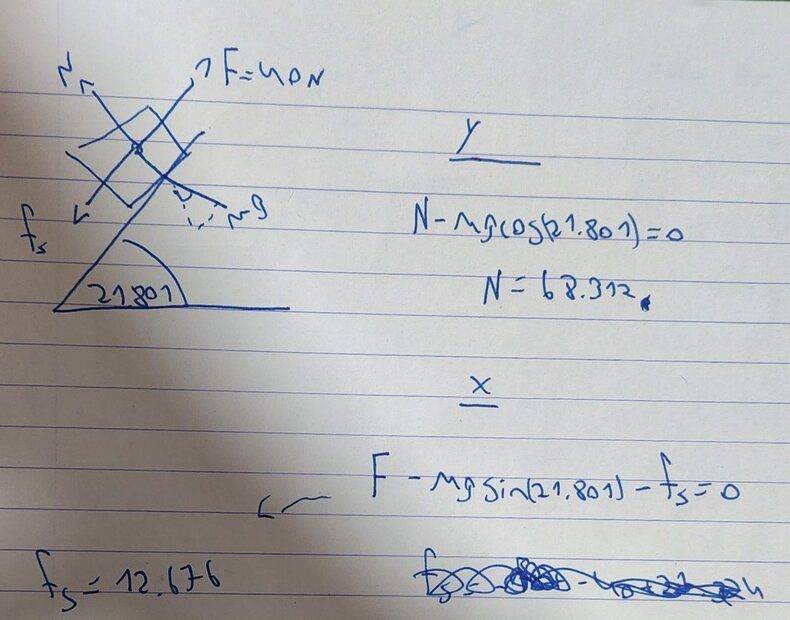
here is my solution i would like to know what I am doing wrong