Heexit
- 10
- 3
- Homework Statement
- Two bodies (masses 2 kg and 4 kg) are joined by a wire. The system is laid along a rough inclined plane (the angle of inclination is 30 degrees). For the upper, lighter body, the coefficient of friction is 0.2 and for the lower it is 0.12. what is the thread force after the system is left to itself?
- Relevant Equations
- F=ma, F=mg, cos, sin,
Hello PhysicsForums!
Here is my attempt at a solution for the problem stated above:
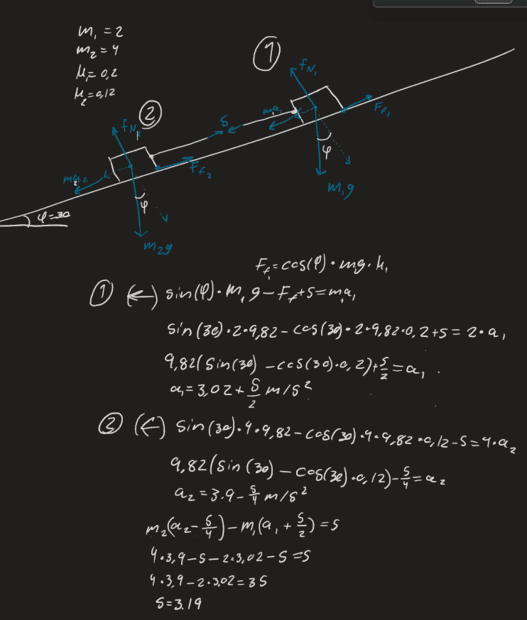
Where m1 and m2 are the masses
Where Ff1 and Ff2 are friction for each mass
Where a1 and a2 is the resulting acceleration
Where S is the fore of the wire (threadforce)
Where FN is the normal force
The answear should be 0.91 Newton
Any clues on what I need to change?
Thanks on beforehand for your help!
Here is my attempt at a solution for the problem stated above:
Where m1 and m2 are the masses
Where Ff1 and Ff2 are friction for each mass
Where a1 and a2 is the resulting acceleration
Where S is the fore of the wire (threadforce)
Where FN is the normal force
The answear should be 0.91 Newton
Any clues on what I need to change?
Thanks on beforehand for your help!