Forces that cause acceleration due to conservation laws

[Soren4]

I find difficulties in identify the forces acting behind the acceleration of objects that are considered consequence of conservation principles (for istance of KE and angular momentum). I'll make an example to explain. The same string-mass system is linked to a rod. In case (a) a force pull the string while the mass is spinning, in case (b) the string goes around the rod as the mass spins. In both cases the mass will accelerate but I'm trying to understand what are the forces behind this acceleration.

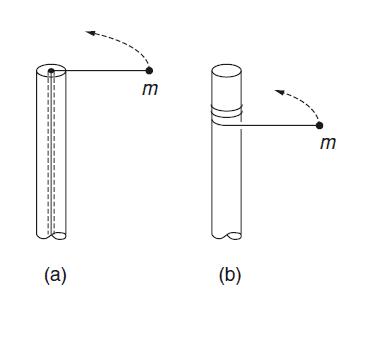
I'm ok with case (a): the force is central and so angular momentum is conserved. The force is not completely radial and the component of the force parallel to displacement change the velocity (in fact kinetic energy is not conserved)

But in case (b) the force is not central and angular momentum is not conserved, while energy is because force is always parallel to the displacement. From the conservation of KE we find that the velocity increases. But which is the force responsible for that? I mean: there must be a force acting in the direction of the displacement if the velocity increases. Where is this force?

 

[Orodruin]

The force is not completely radial and the component of the force parallel to displacement change the velocity (in fact kinetic energy is not conserved)

The force is completely radial in (a), but the velocity is not in the angular direction when you are pulling the string.

 

[Orodruin]

From the conservation of KE we find that the velocity increases.

If kinetic energy is constant, the velocity is constant in case (b). This is also consistent with some quick scribbles I made.

 

[Soren4]

Thanks for your answer! About case (a) I don't see very well how does the force act. It is radial but it is not centripetal. So, using polar coordinates v_r increases, while v_{\theta} remains constant. But if v_{\theta} i constant, if we imagine to look at the circular motion of the mass when the length of the string is \frac{l}{2}, then the velocity of that motion should be the same as the one at the beginning, nevertheless the mass perform a faster circular motion. This imply that v_{\theta} must change but I really do not see why, could you give some further suggestion?

 

[Orodruin]

Thanks for your answer! About case (a) I don't see very well how does the force act. It is radial but it is not centripetal. So, using polar coordinates v_r increases, while v_{\theta} remains constant. But if v_{\theta} i constant, if we imagine to look at the circular motion of the mass when the length of the string is \frac{l}{2}, then the velocity of that motion should be the same as the one at the beginning, nevertheless the mass perform a faster circular motion. This imply that v_{\theta} must change but I really do not see why, could you give some further suggestion?

The velocity in the $\theta$ direction changes due to the motion in the $\theta$ direction. This is always true regardless of whether there are forces acting on an object or not. The reason is that as the object moves, what is the $\theta$ direction changes. For an object moving in a straight line with constant velocity, this means that $v_\theta$ is going to depend on time. In the same fashion, what is the radial direction also changes and so the radial velocity is translated into a velocity in the $\theta$ direction. In order to keep the angular momentum constant, $v_\theta$ will increase as you pull the string.

 

[Soren4]

The velocity in the $\theta$ direction changes due to the motion in the $\theta$ direction. This is always true regardless of whether there are forces acting on an object or not. The reason is that as the object moves, what is the $\theta$ direction changes. For an object moving in a straight line with constant velocity, this means that $v_\theta$ is going to depend on time. In the same fashion, what is the radial direction also changes and so the radial velocity is translated into a velocity in the $\theta$ direction. In order to keep the angular momentum constant, $v_\theta$ will increase as you pull the string.

Thanks for this answer! I got the fact that $\theta$ direction changes but I really don't see how can the radial direction change actually during the motion. Of course the vector $r$ changes but the radial direction is always linking the point to the origin $O$. How can that be?

 

[Orodruin]

Thanks for this answer! I got the fact that $\theta$ direction changes but I really don't see how can the radial direction change actually during the motion. Of course the vector $r$ changes but the radial direction is always linking the point to the origin $O$. How can that be?

Because in order to connect the origin to two different points, you need vectors which point in different directions.