Conservation laws Definition and 114 Threads

In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves over time. Exact conservation laws include conservation of energy, conservation of linear momentum, conservation of angular momentum, and conservation of electric charge. There are also many approximate conservation laws, which apply to such quantities as mass, parity, lepton number, baryon number, strangeness, hypercharge, etc. These quantities are conserved in certain classes of physics processes, but not in all.
A local conservation law is usually expressed mathematically as a continuity equation, a partial differential equation which gives a relation between the amount of the quantity and the "transport" of that quantity. It states that the amount of the conserved quantity at a point or within a volume can only change by the amount of the quantity which flows in or out of the volume.
From Noether's theorem, each conservation law is associated with a symmetry in the underlying physics.

View More On Wikipedia.org
Recent contents Top users
  1. N

    Partial differential equations, symmetries, invariants, conservations,

    I know the method is involving adjoint equation, lagrange functional and conserwation laws but i dont know how to do it, please help! I know something like this: that we must split our function into two F=(F_1,F_2), also u=(u_1,u_2) and v=(v_1,v_2) and we must calculate adjoint equation F* and...
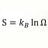
  2. morrobay

    B Quantum Nonlocality or Non Counterfactual Definiteness?

    It seems the major premise for the derivation of Bell Inequalities is Counterfactual Definiteness for both electrons and photons : For electrons the spins at x, y, z directions are expected from conservation laws. See table. And for photons the eight polarization types along three orientations...
  3. M

    Box on treadmill connected to a spring

    First i show the sketch of the setup: My first attempt was just to balance out the forces on the box. On the sketch below i have shown the situation where the spring is stretched distance L. In this situation we get the equations: Which when solved leads to All good. I then looked at the...
  4. S

    A Conservation Laws from Continuity Equations in Fluid Flow

    Consider a fluid flow with density ##\rho=\rho(t,x)## and velocity vector ##v=v(t,x)##. Assume it satisfies the continuity equation $$ \partial_t \rho + \nabla \cdot (\rho v) = 0. $$ We now that, by Reynolds Transport Theorem (RTT), this implies that the total mass is conserved $$...
  5. S

    I Deviations of conservation laws in cosmological evolution?

    If energy is "not conserved" in General Relativity (or at least, it is difficult to define it) in the context of an expanding accelerating spacetime (like it happens in our Universe), are there any observations of deviations from the strict conservation laws in the evolution and formation of...
  6. M

    B Why is KE not conserved when momentum is?

    Its clear in elastic collision that both KE and momentum is conserved. Bodies exchange their velocities. It is seen clearly in this video. There is no decrease in speed. Total KE is constant. But in an inelastic collision momentum is conserved again but not the KE. There is loss in KE (I guess...
  7. S

    A Does Spacetime Absorb Energy in General Relativity?

    Some physicists prefer to explain the problem of conservation of energy in General Relativity by considering the gravitational potential energy of the universe that would cancel all the other energies and therefore the energy in the universe would be conserved this way. However, many other...
  8. casualguitar

    Modelling of two phase flow in packed bed (continued)

    Previous post linked here, where a model for the two phase flow of air through a packed bed was developed: https://www.physicsforums.com/threads/modelling-of-two-phase-flow-in-packed-bed-using-conservation-equations.1008754/ The first few comments on this new thread will be copies of the...
  9. casualguitar

    Modelling of two phase flow in packed bed using conservation equations

    Previously, I have seen the derivation of the energy conservation equations for simulation of single phase flow in a porous media (a packed bed). These are the energy equations for the solid and fluid respectively: I understand the derivation, however, these equations will only work when the...
  10. S

    B Conservation Laws & General Relativity: Understanding Energy

    How does general relativity shows the conservation of energy. Because I was reading and listening to something today that touched on this subject. It almost seems as though if you scale GR to larger sizes it stops working and turns into an incomplete law of nature like Newton's laws of gravitation.
  11. PiEpsilon

    Elastic collision of particle and rotating disc

    Consider the system of the mass and uniform disc. Since no external forces act on the system, the angular momentum will be conserved. For elastic collision, the kinetic energy of the system stays constant.Measuring angular momentum from the hinge: ##\vec L_i = Rmv_0 \space\hat i + I \omega_0...
  12. F

    Annihilation: calculation of photon energies

    I set up this problem this way: ##p_a^{\mu}=(E, \sqrt{E^2-m^2}, 0, 0)## ##p_b^{\mu}=(m, 0, 0, 0)## ##p_c^{\mu}=(2E_\gamma, 2E_\gamma, 0, 0)## I have chosen to consider the two photons as a single particle of energy equal to ##2E_\gamma##. At this point I applied conservation of the...
  13. S

    A What would it mean if symmetries in physics would not be fundamental?

    Physicist Joseph Polchinski wrote an article (https://arxiv.org/pdf/1412.5704.pdf) where he considered the possibility that all symmetries in nature may not be fundamental. He says at page 36: "From more theoretical points of view, string theory appears to allow no exact global symmetries, and...
  14. Hamiltonian

    Conservation of Linear Momentum and Energy in a Two-Block System

    since there is no external force in the x-direction linear momentum can be conserved. Hence I get the equation $$0 = mv^2 - 9mV^2$$ where ##v## is the velocity of B towards the right and ##V## is the velocity of A toward the left. also the conservation of energy gives $$1/2(9m)V^2 + (1/2)mv^2 =...
  15. Like Tony Stark

    Two rods, each with a free and a fixed ball and a spring

    Since there are no external forces, the angular momentum (##L##) and linear momentum (##P##) are conserved. Let's call the left rod ##A## and the right one ##B##. If all the balls were fixed, I'd write ##L_0=L_f## ##L_A+L_B=(I_A+I_B)\omega_f## From this equation I can find the final angular...
  16. Like Tony Stark

    Conservative forces vs friction

    Hello I've written that homework statement as an example to illustrate my doubt: How can I tell if a force is conservative or not? I've read that, if the curl of the force is 0, it's conservative. But what about the friction force (##f=\mu N##)? Its curl is also zero, but it's not conservative...
  17. T

    Isospin Conservation: Calculating I3 and I

    I got the I3 values for the tau(minus) to be -1, as charge is -1 and Y=0. For muon(minus) i got I3 to be -1 too using the same equation and the anti electron neutrino to have an isospin of zero (since Q=0, Y=0). This shows I3 to be conserved (which is needed for strong interaction i believe)...
  18. G

    I Do collapse interpretations respect conservation laws?

    Hi. As far as I know, during the unitary evolution of quantum states, conservation laws are respected. Obviously this can't be true for the measurement process, if we only look at the system and exclude the observer. Now the simple explanation I've heard about this is that in quantum mechanics...
  19. isabelle3

    A bullet hits a rod attached to a pivot at one of its ends....

    My initial thought was to use the conservation of energy law since there're no external forces acting on the system bullet + rod. The rod is in rest, the bullet is moving. Then after the collision, the bullet and the rod are rotating around the pivot together, so the kinetic energy of the bullet...
  20. L

    How Does Faraday's Law Impact Momentum Conservation in a Magnetic System?

    Hello to all. Second post here so I apologise if I post to the wrong place with wrong altitude etc We have a schematic of a problem like here: https://www.physicsforums.com/threads/conducting-rod-is-free-to-move-over-a-loop-under-influence-of-b-field.750763/ The conducting rod ab shown in the...
  21. KingOfDirewolves

    Classical Mechanics Problem Based On Conservation Of Energy

    I have tried using Conservation of Energy but I'm getting incorrect answer.
  22. M

    Conservation laws in Newtonian and Hamiltonian (symplectic) mechanics

    In Newtonian mechanics, conservation laws of momentum and angular momentum for an isolated system follow from Newton's laws plus the assumption that all forces are central. This picture tells nothing about symmetries. In contrast, in Hamiltonian mechanics, conservation laws are tightly...
  23. mPlummers

    I Forbidden decays and conservation laws

    Problem Statement: Hello! I'm trying to learn how to know if a particular interaction is allowed or forbidden. I found 3 decays which i can't understand. Relevant Equations: The decays are: 1) \eta \rightarrow \pi ^{0}+\gamma 2) \phi \rightarrow \rho^{0}+\gamma 3) \eta \rightarrow \pi...
  24. Abhishek11235

    Solving this problem using the energy method

    I attempted the solution using force method. I got correct. However, I was stuck at the alternative way to solve problem using energy method. As shown in screenshot 2, he tells that the energy of system changes due to 2 ways: - The tension T - Leaking of mass As shown in screenshot 2 ,the...
  25. Harperchisari

    The energy conservation issue with parallel charged plates with a hole.

    A while back I thought of an issue with parallel charged plates. Imagine this: a set of opposite charged resistive plates with holes in the center. In theory, there is a finite amount of energy required to push a positive charged particle through the hole in the positive plate (in theory it...
  26. F

    Calculating Centripetal Acceleration in a Vertical Loop

    $$mg(0.45) = mg(R + R \cdot cos(\frac{π}{3})) + \frac{1}{2}mv^2$$ $$v^2 = g(0.9 - 3R)$$ The centripetal acceleration during the "flying through air" will be given by gravity $$mg \cdot cos(\frac{\pi}{3}) = \frac{mv^2}{r}$$ $$R = \frac{1.8}{5}$$ But my book says $$ R = \frac{1}{5}$$
  27. ?

    Rotating sphere which separates into hemispheres

    Hi all, The scenario I'm considering is a solid sphere (of uniform density) rotating with constant angular velocity when it abruptly splits into two hemispheres along a cut which contains the rotation axis. The hemispheres will begin to separate; if, for example, we consider the rotation to be...
  28. stevendaryl

    A Intuitive Meaning of the Coleman-Mandula Theorem

    This theorem is summarized here: https://en.wikipedia.org/wiki/Coleman%E2%80%93Mandula_theorem I sort of understand the mathematical content of the theorem, that But what I don't understand is, intuitively, what sort of possibilities are ruled out. I've heard it said that flavor conservation...
  29. L

    Relativistic Dynamics Problem - Reference Frames

    Homework Statement Two images are attached. The first image details the problem. The second image has an x',y' coordinate system depiction of the problem. Homework Equations The total energy of a particle is defined as E = mc^2, with m = γ*m_0. The Attempt at a Solution If the x', y'...
  30. Phylosopher

    Conservation laws from Lagrange's equation

    My question is related to the book: Classical Mechanics by Taylor. Section 7.8 So, In the book Taylor is trying to derive the conservation of momentum and energy from Lagrange's equation. I understood everything, but I am struggling with the concept and the following equation...
  31. Lukeblackhill

    Symmetries and Conservation Laws

    I've been caught by a quite interesting statement of Berkeley physics Course Vol.1 (Chap. 5), that says "In the physical world there exist a number of conservation laws, some exact and some approximate. A conservation law is usually the consequence of some underlying symmetry in the universe."...
  32. Manolisjam

    3 balls in a moving mechanics problem

    Homework Statement Consider 2 balls A,B on the same line . and they are connected to a third one G with a rope L. AG, AB. now the system monves in the effect of the mass of G and its projection to the line AB is in the middle. No friction. mass of A=mass of B=m and mass of G=2m .FInd the time...
  33. Manolisjam

    Classical Mechanics Problem with balls

    Homework Statement Consider 2 balls A,B on the same line . and they are connected to a third one G with a rope L. AG, AB. now the system monves in the effect of the mass of G and its projection to the line AB is in the middle. No friction. mass of A=mass of B=m and mass of G=2m .FInd the time...
  34. R

    Elastic and inelstic collisions conceptual questions.

    Homework Statement The questions showed in the pictures ask me whether the collisions in the drawings could be elastic or inelastic, I am not given any mass, the angles are a little vague but I think B and C are supposed to be π/2 and π respectively. For velocity, I am just given the direction...
  35. J

    Conserved quantity for a particle in a homogeneous and static magnetic field

    The equation of motion for a charged particle with mass ##m## and charge ##q## in a static magnetic field is: ##\frac{d}{dt}[m{\dot{\vec{r}}}]=q\ \dot{\vec{r}}\times \vec{B}## From this, we can see that ##\frac{d}{dt}[m\dot{\vec{r}}-q \vec{r}\times \vec{B}]=0## and so the following quantity is...
  36. parshyaa

    I What does Noether's theorem actually say?

    I don't know much about classical physics(such as lagrangian function), but as i was reading conservation of energy, i came to this theorem and it tells that if a system is symmetrical in certain transformations(such as translation, rotation etc) then it will have a corresponding law of...
  37. entropy1

    Photon absorbtion and conservation

    If a (polarized) photon is absorbed by a polarization filter, does its energy go into the filter? I am wondering if that is the case to obey conservation laws. And if it passes, is its original polarisation direction somehow conserved?
  38. S

    I What is the Conservation of Information in Quantum Mechanics?

    Hi everyone, I was watching Susskinsd's lectures posted on youtube about Quantum mechanics and he started explaining his -1st basic law of physics saying: the conservation of information means basically that if you start with 2 quantum states (vectors) which are observably different, or...
  39. LarryS

    I Conservation laws during particle decay?

    I believe that conservation laws, like for energy and momentum, are obeyed during the particle decay process, e.g. the total energy of the new output particles is equal to the energy of the one input particle. But is that relationship subject to quantum fuzziness? Suppose we, somehow, prepare...
  40. R

    I Compton effect: how can it take place?

    English is not my native language. So, I hope to be understood. :-) The Compton effect is the dynamics in which high-energy incident photons (X or gamma) are scattered by electrons of certain materials, like graphite. The electrons are supposed to be free, as they are only weakly bounded by...
  41. GamrCorps

    Conservation of momentum/energy of stacked balls

    Homework Statement A tennis ball and basketball are dropped from a height of 1m (the tennis ball on top of the basketball). The tennis ball has a mass of 75g and the basketball has a mass of 1kg. When dropped separately, the tennis ball bounces to a height of 0.5m and the basketball to a...
  42. E

    Conserved quantities in the Korteweg-de Vries equation

    Homework Statement Consider the Kortweg-de Vires Equation in the form $$\frac{\partial \psi}{\partial t}+\frac{\partial^3 \psi}{\partial x^3}+6\psi\frac{\partial \psi}{\partial x}=0$$ Find the relation between the coefficients ##c## and ##d## , such that the following quantity is conserved...
  43. S

    A What Are the Possible Decay Processes of the W⁻ Boson?

    The decay processes of the ##W## bosons are completely governed by the charged current interaction terms of the Standard model: $$\mathcal{L}_{cc} = ie_{W}\big[W_{\mu}^{+}(\bar{\nu}_{m}\gamma^{\mu}(1-\gamma_{5})e_{m} + V_{mn}\bar{u}_{m}\gamma^{\mu}(1-\gamma_{5})d_{n})\\...
  44. S

    Air-Track Carts & Spring (Energy)

    Homework Statement The air-track carts in the figure(Figure 1) are sliding to the right at 2.0 m/s. The spring between them has a spring constant of 140 N/m and is compressed 4.1 cm. The carts slide past a flame that burns through the string holding them together. What is the final speed of...
  45. F

    A How Do Conservation Laws Apply to a 4 Current in General Relativity?

    Consider a 4 current J^\mu and a metric g then conservation laws will require \del_\mu J^\mu = 0 my lecturer gave me a brief problem and I think I'm missing some understanding of it he writes What I'm not understanding is, where he states, if we choose B to be the time slice between etc...
  46. M

    Conservation laws in rotational movement

    Homework Statement Consider a uniform rod of mass 12kg and length 1.0m. At it's end the rod is attached to a fixed, friction free pivot. Initially the rod is balanced vertically above the pivot and begins to fall (from rest) as shown in the diagram. Determine, a) the angular acceleration of...
  47. G

    Field-free formulation of ED: Conservation laws?

    Hi. In the (mainstream) books of electrodynamics I know, the electric and magnetic fields are introduced as force fields normalized to a charged test particle of 1 C. This makes those fields appear as an unnecessary, but convenient mathematical tool. They cannot be measured in the absence of...
  48. S

    Forces that cause acceleration due to conservation laws

    I find difficulties in identify the forces acting behind the acceleration of objects that are considered consequence of conservation principles (for istance of KE and angular momentum). I'll make an example to explain. The same string-mass system is linked to a rod. In case (a) a force pull the...
  49. P

    I Understanding Hamiltonian Conservation Laws

    I'm a little confused about the hamiltonian. Once you have the hamiltonian how can you find conserved quantities. I understand that if it has no explicit dependence on time then the hamiltonian itself is conserved, but how would you get specific conservation laws from this? Many thanks
  50. emeriska

    LRC equation using Poynting theorem and conservation laws

    Homework Statement We have an ordinary LRC circuit with inductance L, capacitance C and resistance R with an oscillating voltage with low frequency (U^e). Using the energy conservation law and Poynting's theorem, find the differential equation: $$L \frac{\partial ^2}{\partial t^2}I + R...
Back
Top