Form of function over interval

[JulieK]

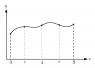
I know $y$ is a function of $x$ [i.e. $y=f\left(x\right)$]
with two known boundary conditions, that is $f\left(x=A\right)=C$
and $f\left(x=B\right)=D$ where $C$ and $D$ are known constants
(please see figure). I do not know the form of this function and therefore
I am trying to find the form of $y$ as a function of $x$ over the
whole interval $A<x<B$. I have an additional condition that is if
I discretize the interval I can obtain the folowing relation

$g(A,c)=g(c,d)=g(d,e)=g(e,B)=E$

where $g$ is a known function of the given arguments and $E$ is
a known constant. I think this problem can be solved by using the
variational principle possibly with the use of Lagrange multipliers.
I did some initial attempts but I am not sure about the results. Can
you suggest a method (variational or not) that can solve this problem
so that we can obtain the form of $y$ as a function of $x$ over
the whole interval.

Many thanks in advance!

 

[JulieK]

I should have added

$g(A,B)=g(A,c)=g(c,d)=g(d,e)=g(e,B)=E$

 

[mathman]

You need to describe the relationship between f and g.

 

[JulieK]

I made a mistake in the problem description. The additional condition is:

$g(y(A),y(B))=g(y(A),y(c))=g(y(c),y(d))=g(y(d),y(e))=g(y(e),y(B))=E$

Sorry about this!