A Forward-in-time analysis of delayed-choice entanglement swapping

[DrChinese]

The correlation not present in the Ma-X experiment is correlation between Victor's Φ- result, and Alice's and Bob's measurement in the other two unbiased bases, H/V and +/-.

...

In the Ma-X experiment, if* Victor observes Φ- (and he cannot ever observe Φ+) then he knows if Alice and Bob measured in the R/L basis, they will be correlated (trivially so, they must be LL).
...

OK, first where we agree: We are specifying measurement of 1 & 4 on one basis, and measurement of 2 & 3 on some other unbiased basis.

Now, it was you who turned me on to understanding Mjelva's logic. He says in that situation: Once you know the 1 & 4 outcomes (say up-up, per his 9A for example), then the 2 & 3 BSM (swap) is via selection where Φ- can result. That matches experiment and would, in fact have the effect of delivering the proper results for both BSMs and for SSMs. So that is not the point of disagreement.

And how that happens, according to the forward in time only view: If we know 1 & 4 are LL - or up-up in Mjelva's (9A) - then a Φ- BSM is compatible, but not a Φ+ BSM. But again: when we have the Ma-X version, we know 1 & 4 are LL (or up-up) just as before. Your problem is: A Φ- BSM is an actual compatible outcome, but equally frequent is a Φ+ BSM experimental outcome. This is diametrically opposed to what you assert, and is also opposed to what Mjelva claims in his (9A).

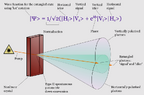
I am flat out saying that's what happens, and you are exactly incorrect as to what experiment shows. Because if it didn't, Type II polarization entangled PDC sources would not need to overlap the V and H cones as shown in the diagram. If they didn't overlap, it would be my Ma-X version. But we also know that doesn't lead to entanglement swapping. Surely you can agree with this point - there is nothing controversial about it. You need 1 & 2 to be initially polarization entangled (anti-correlated) to get entanglement swapping in this regime. That entangled state is qualitatively different than an initial state of up-down (or whatever). That accounts for the results being different; so the evolution cannot work as you describe.

So... that's our point of departure - and we should focus on this and nothing else for now. The state evolution cannot be as you describe below, because my Ma-X example follows that but yields the wrong prediction (using your logic). What I am applying to get that wrong prediction, verbatim:

$$\begin{eqnarray*}I_{14}\otimes U_{23}\ket{LL}_{14}\ket{RR}_{23} &=& \ket{LL}_{14}\otimes(U_{23}\ket{RR}_{23})\\
&=&\ket{LL}_{14}\otimes(U_{23}\ket{\phi^-}_{23} +iU_{23}\ket{\psi^+}_{23})/\sqrt{2}\end{eqnarray*}$$
Nope. Actual results include both Φ+ and Ψ- terms.

 

[eloheim]

So... that's our point of departure - and we should focus on this and nothing else for now. The state evolution cannot be as you describe below, because my Ma-X example follows that but yields the wrong prediction (using your logic). What I am applying to get that wrong prediction, verbatim:

$$\begin{eqnarray*}I_{14}\otimes U_{23}\ket{LL}_{14}\ket{RR}_{23} &=& \ket{LL}_{14}\otimes(U_{23}\ket{RR}_{23})\\
&=&\ket{LL}_{14}\otimes(U_{23}\ket{\phi^-}_{23} +iU_{23}\ket{\psi^+}_{23})/\sqrt{2}\end{eqnarray*}$$
Nope. Actual results include both Φ+ and Ψ- terms.

So in the Ma-X version, even if Alice and Bob "measure" in the prepared basis (if we already know their photons are L and L there's no point in measuring, right?) the result of Victor putting 2 and 3 into a bell state by making them indistinguishable will produce different results than the original Ma setup?

Just going through the math for the other combinations has Φ- only being produced from LL, RR, +-, and Φ+ only from ++, --, LR.

 

[Morbert]

And how that happens, according to the forward in time only view: If we know 1 & 4 are LL - or up-up in Mjelva's (9A) - then a Φ- BSM is compatible, but not a Φ+ BSM. But again: when we have the Ma-X version, we know 1 & 4 are LL (or up-up) just as before. Your problem is: A Φ- BSM is an actual compatible outcome, but equally frequent is a Φ+ BSM experimental outcome. This is diametrically opposed to what you assert, and is also opposed to what Mjelva claims in his (9A).

As described by Ma, $\ket{L} = (\ket{H} - i\ket{V})/\sqrt{2}$, and so $$\bra{\phi^+}LL\rangle = 0$$That holds however $\ket{LL}$ was prepared, so a BSM carried out on a system prepared as $\ket{LL}$ cannot yield $\phi^+$. This is a constraint imposed directly by the theory/the orthogonality of the states, and is not dependent on the specifics of the preparation or the measurement apparatus. Any BSM on $\ket{LL}$ that yields both $\phi^+$ and $\phi^-$ is either i) Not a BSM or ii) contradicts quantum mechanics. Show me such a scenario in literature. It is not the case in the original Ma experiment, and it is not the case in the Type II PDC described by Kwiat et al.

 

[DrChinese]

So in the Ma-X version, even if Alice and Bob "measure" in the prepared basis (if we already know their photons are L and L there's no point in measuring, right?) the result of Victor putting 2 and 3 into a bell state by making them indistinguishable will produce different results than the original Ma setup?

Just going through the math for the other combinations has Φ- only being produced from LL, RR, +-, and Φ+ only from ++, --, LR.

Yes, it produces distinctly different results. There is a qualitative difference between an entangled state before all measurements are completed, and a state with specific outcomes. But according to the evolution as presented by Mjelva (see his 9A especially, showing specific outcomes before all measurements completed): it should produce the same results. You might ask: Why does this experimental difference matter?

The entire premise of the forward in time only hypothesis - which by the way is completely reasonable - is: Once a measurement is performed, and a possible quantum outcome is selected (by random chance of course), then there can be no additional connection with the quantum components so measured. In Ma, those are photons 1 & 4; while in Megidish, it's only photon 1.

Mjelva: "So we see that on projection-based accounts, the projection ensures that there can be no entanglement between particle 1 and particle 4, and thus rules out timelike entanglement as an explanation of the observed correlations."

But that is not how the actual predictions are generated in the quantum world. A full 4-fold quantum context is required to properly model and predict entanglement swapping outcomes and outcome statistics. And such context is not limited to regions of spacetime constrained by Einsteinian locality or causality, as .

Ma: They start with (1) which is agreed by everyone. But their post-swap state (2) is a 4 photon state which does not resemble the presentation of Mjelva's (9). They say photons 1 & 4 become entangled after the fact. "Consequently photons 1 (Alice) and 4 (Bob) also become entangled [after the fact] and entanglement swapping is achieved. ... Note that after the entanglement swapping, photons 1&2(and 3&4) are not entangled with each other anymore, which manifests the monogamy of entanglement."

Megidish: They also start with (1), and their post-swap state (3) is the same as Ma's. Their characterization is likewise distinctly in opposition: "When the two photons of time τ (photons 2 and 3) are projected onto any Bell state, the first and last photons (1 and 4) collapse also into the same state and entanglement is swapped. The first and last photons, that did not share between them any correlations, become entangled."

When the Ma, Megidish, Hensen experimental teams design their experiments, they cannot use the Mjelva forward only projection logic. Why? It's simply wrong (as I demonstrated based on the cited papers). They are setting out to experimentally disprove that "semi-classical" thinking anyway. Unfortunately, their experiments are specifically designed to highlight only a single particular variation of the quantum time ordering/nonlocality issues. Accordingly, you must look from paper to paper to get a full understanding of the quantum rules.


Note: The Megidish experiment (Ma too) has always seemed to me to be one of the most radical examples of the strange role of ordering in the quantum world. I started a thread here on it the day it appeared in 2012 . Since then, it seems to have mostly been of interest to other experimenters and researchers, and I consider it generally accepted science at this point. But I have seen very little about it online. So I was very happy to see Mjelva's detailed attempt to tear into it, even though his analysis is ultimately flawed (IMHO of course - each person must decide for themself).

 

[DrChinese]

1. As described by Ma, $\ket{L} = (\ket{H} - i\ket{V})/\sqrt{2}$, and so $$\bra{\phi^+}LL\rangle = 0$$That holds however $\ket{LL}$ was prepared, so a BSM carried out on a system prepared as $\ket{LL}$ cannot yield $\phi^+$.

This is a constraint imposed directly by the theory/the orthogonality of the states, and is not dependent on the specifics of the preparation or the measurement apparatus.

2. Any BSM on $\ket{LL}$ that yields both $\phi^+$ and $\phi^-$ is either i) Not a BSM or ii) contradicts quantum mechanics.

3. Show me such a scenario in literature. It is not the case in the original Ma experiment, and it is not the case in the Type II PDC described by Kwiat et al.

1. All of your statements are completely wrong, as you hold onto a physical point that cannot be supported. You have yet to present any kind of support for your thinking, other than Mjelva's words (obviously not a suitable reference). Here's what he says (swap is not real) versus what top teams say (swaps are real):

Mjelva: "So we see that on projection-based accounts, the projection ensures that there can be no entanglement between particle 1 and particle 4, and thus rules out timelike entanglement as an explanation of the observed correlations."

Ma: "Consequently photons 1 (Alice) and 4 (Bob) also become entangled [after the fact] and entanglement swapping is achieved. ... Note that after the entanglement swapping, photons 1&2(and 3&4) are not entangled with each other anymore, which manifests the monogamy of entanglement."

Megidish: "When the two photons of time τ (photons 2 and 3) are projected onto any Bell state, the first and last photons (1 and 4) collapse also into the same state and entanglement is swapped. The first and last photons, that did not share between them any correlations [or coexistence], become entangled."


2. How can it not be a BSM? It exactly fits your definition of a BSM. Anyway, it does project photons 2 & 3 into an entangled state, either Φ+ or Φ- equally.


3. As already stated: Every single experiment ever performed using Type II PDC sources to create polarization entangled photons for entanglement swapping is a demonstration of what I say. I already cited something from 1995 by a Zeilinger team showing the details of Type II. The Ma and Megidish experiments use that technique to create Ψ- pairs. If source pairs useful for swapping could be created without the requirement of overlapping the Vertical and Horizontal cones (and taking the small indistinguishable cross-section), then why do they bother to do all this extra work?

Obviously, they get different results when they pull pairs outside the Vertical and Horizontal overlapping regions. And you already agree that the evolution should be the same, and therefore not produce different results.

 

[Morbert]

@DrChinese You are denying basic textbook relations in QM. Relations that are necessary if we are to show that a forward-in-time analysis, consisting of textbook unitary evolutions and textbook state reductions, can reproduce the frequencies and correlations observed in any of these experiments, from Ma's to Megidish's to Hensen's.

For example, it is not "completely wrong" that $\bra{\phi^+}LL\rangle = 0$, and hence a BSM carried out on a system prepared as $\ket{LL}$ cannot yield the outcome $\phi^+$. It can be plainly shown.

 

[PeterDonis]

$\ket{LL}$ was prepared

What is your basis for this statement?

 

[Morbert]

What is your basis for this statement?

It is the premise supposed in the Ma-X experiment.

 

[PeterDonis]

It is the premise supposed in the Ma-X experiment.

Where, specifically, in the Ma paper does it state this premise?

 

[Morbert]

Where, specifically, in the Ma paper does it state this premise?

Ma-X, not Ma. See @DrChinese's earlier posts. It is his modification.

 

[PeterDonis]

Ma-X, not Ma. See @DrChinese's earlier posts. It is his modification.

Which post, specifically? This thread is getting pretty long.

 

[Morbert]

Which post, specifically? This thread is getting pretty long.

https://www.physicsforums.com/threa...ce-entanglement-swapping.1078114/post-7241224

Under this modified setup, the four photons are prepared in the state $\ket{LL}_{23}\ket{RR}_{14}$ result $\phi^+$ is not possible as $\bra{\phi^+}LL\rangle = \bra{\phi^+}RR\rangle = 0$.

[edit] - Actually rereading, the initial state was $\ket{LL}_{14}\ket{RR}_{23}$. Though the same consequences follow from either $\ket{RR}$ or $\ket{LL}$

 

[PeterDonis]

https://www.physicsforums.com/threa...ce-entanglement-swapping.1078114/post-7241224

Under this modified setup, the four photons are prepared in the state $\ket{LL}_{23}\ket{RR}_{14}$ result $\phi^+$ is not possible as $\bra{\phi^+}LL\rangle = \bra{\phi^+}RR\rangle = 0$.

[edit] - Actually rereading, the initial state was $\ket{LL}_{14}\ket{RR}_{23}$. Though the same consequences follow from either $\ket{RR}$ or $\ket{LL}$

This involves a setup in which there is no entanglement prepared; the four-photon state prepared is completely separable. So of course there can't be any entanglement swapping, since there is no entanglement to swap. So of course no Bell state of any pair of the photons can be output.

But of course this is not the same as an entanglement swapping experiment, where the four photons are not prepared in a completely separable state. @DrChinese was obviously not intending this "Ma-X" variation to be relevant to an analysis of entanglement swapping. He was intending it to illustrate what happens where there is no entanglement swapping possible.

 

[eloheim]

This involves a setup in which there is no entanglement prepared; the four-photon state prepared is completely separable. So of course there can't be any entanglement swapping, since there is no entanglement to swap. So of course no Bell state of any pair of the photons can be output.

But of course this is not the same as an entanglement swapping experiment, where the four photons are not prepared in a completely separable state. @DrChinese was obviously not intending this "Ma-X" variation to be relevant to an analysis of entanglement swapping. He was intending it to illustrate what happens where there is no entanglement swapping possible.

I believe it is the point being discussed right now though. You can put 2+3 into a bell state whether they come from entangled pairs or not, and the question is whether the results are the same as the real experiment. I think we all agree that if Alice and Bob are allowed to measure on a different basis then Victor's results won't match, but I think DrChinese is saying the results won't match the real experiment even if Alice and Bob measure in the prepared basis.

I also think DrChinese is saying if you follow Mjelva's math (like his equations 5 or 9) you should get results incompatible with experimental reality but I'm still trying to parse that.

 

[PeterDonis]

You can put 2+3 into a bell state whether they come from entangled pairs or not

You're missing the point. If all four photons are in a completely separable state, which is the premise @Morbert was talking about, then you cannot entangle anything using the configuration in the experiments under discussion. You can only put 2+3 into a Bell state if the pairs 1+2 and 3+4 start out in Bell states and you then do an entanglement swap.

 

[Morbert]

@DrChinese's goal is to demonstrate that Mjelva's forward-in-time analysis - an analysis which eliminates entanglement swapping in the sense that Victor's BSM projects onto a state where photons 1 & 4 are still separable/not entangled - leads to contradictions with what is observed in experiments. The Ma-X variation is intended to bring focus to such contradictions.

The impasse we have reached is that DrChinese believes if the initial 4 photons are prepared in the sate $\ket{LL}_{14}\ket{RR}_{23}$, then "In the Ma-X scenario: there is no correlation between the $\ket{LL}_{14}$ outcomes and the $\ket{\phi^-}_{23}$ outcomes versus the $\ket{\phi^+}_{23}$ outcomes." and " A $\phi^-$ BSM is an actual compatible outcome, but equally frequent is a $\phi^+$ BSM experimental outcome" yet when I work through this variation, I show that $\ket{\phi^+}_{23}$ outcomes cannot actually occur, as $\bra{\phi^+}RR\rangle_{23} = \bra{\phi^+}LL\rangle_{23} = 0$.

 

[PeterDonis]

an analysis which eliminates entanglement swapping in the sense that Victor's BSM projects onto a state where photons 1 & 4 are still separable/not entangled

But this would disagree with the actual experimental results.

 

[Morbert]

But this would disagree with the actual experimental results.

See equations 5a-5d in Mjelva. Projection onto states like these will correctly predict experimental results. These states have no entangled 1 & 4 pairs.

Mjelva's 4.1.1 analysis is quite general. I have applied this to the cases where Alice and Bob measure photon polarization in the H/V or L/R basis, which greatly simplifies things.

 

[DrChinese]

I believe it is the point being discussed right now though. You can put 2+3 into a bell state whether they come from entangled pairs or not, and the question is whether the results are the same as the real experiment. I think we all agree that if Alice and Bob are allowed to measure on a different basis then Victor's results won't match, but I think DrChinese is saying the results won't match the real experiment even if Alice and Bob measure in the prepared basis.

I also think DrChinese is saying if you follow Mjelva's math (like his equations 5 or 9) you should get results incompatible with experimental reality but I'm still trying to parse that.

This is what I am asserting. Specifically:

Mjelva (and Morbert) claim there is a forward in time only evolution of quantum states that provides a viable description of swapping experiments. In the examples such as his formulae (pre-8), (8) and (9), that is presented and superficially appears correct. Note that everyone agrees that the initial 4 photon state is something like:

|Ψ->₁₂ ⊗ |Ψ->₃₄ (1)

Ma & Megidish and everyone else presents the next step of the evolution (swap=on) as being the result of a BSM. That post-swap state is of course one of the 4 Bell states, here per Ma's (2) and Megidish's (3):

|Ψ〉₁₂₃₄= ½(|Ψ+〉₁₄⨂|Ψ+〉₂₃ − |Ψ−〉₁₄⨂|Ψ−〉₂₃ − |Φ+〉₁₄⨂|Φ+〉₂₃ + |Φ−〉₁₄⨂|Φ−〉₂₃) (2)

But that is NOT the same evolution as Mjelva describes at all. The Ma/Megidish evolution goes directly from my (1) to my (2) without Mjelva's intermediate steps for each element of the measurement process. That's because timing/order of the intermediate measurements is not a factor in the final quantum state post-BSM (swap). As a result, Mjelva ends up with an intermediate state like his (8) in which there is an "A" fork and a "B" fork. He states explicitly: "Unlike in ordinary entanglement swapping-experiments, this does not project the pair (1,4) into a Bell state..." Whoops, this assertion is diametrically opposed to what Ma says: "Consequently photons 1 (Alice) and 4 (Bob) also become entangled and entanglement swapping is achieved..." so we have our point of departure.

Mjelva's intermediate presentation pre-BSM (8A) goes to post-BSM (9A), and he claims this evolution is what actually occurs. That's the hypothesis anyway, and it is subject to experimental confirmation. Well, it is easily possible to test that! If you start with a quantum state of his (8A), you simply perform the BSM and see if what you get is his (9A). For example: If you measured photons 1 & 4 as up-up, then Mjelva says that you can see the Φ- BSM signature about half the time, and the Φ+ BSM signature not at all. But in the real world, this does NOT happen.

To prove this, merely start with source photons 1 & 4 being in the up-up state (a la 8A) and perform a BSM on photons 2 & 3. If Mjelva is correct and there is no such thing as 1 & 4 being cast after the fact (as in Ma's experiment) into an entangled state, this should yield the results per Mjelva's (9A). That's can't happen, because a BSM on such a state produces both Φ- BSM signatures and Φ+- BSM signatures equally. That's because photons 1 & 2 must be in a polarization entangled state to start with, which is qualitatively different than Mjelva's (8A) - which actually is NOT an intermediate step in the quantum state evolution.

Note that there are no actual papers demonstrating this exact experimental point as I describe in the paragraph above, you must deduce that result from the Ma/Megidish experiments indirectly. Both of these experiments use Type II PDC to create polarization entangled pairs. But that requires an important element during setup: you must select pairs from a very precise overlapping portion of the cones (see the diagram in various posts above). If they didn't do that, the resulting source photons will have known and separable states. A simple manipulation will then produce the desired up-up results for photons 1 & 4. And according to Mjelva, the results (post measurement of photons 1 & 4 but before the BSM on photons 2 & 3) would be exactly per his (9A). Were that true, we would simply ask the Ma team why they both to capture from the overlapping regions. Why not instead save yourself the time and effort to overlap, since the evolution after a BSM will be identical?

Answer: The evolution from (8A) to (9A) does not occur. Mjelva is simply wrong on this point. It looks good in his paper, but it won't work if (8A) is re-created in practice using unentangled sources for either 1&2 or 3&4. What's good for the goose is good for the gander (i.e. you can't pick and choose when to apply your premise - either 8A goes to 9A or it doesn't). Neither Ma, nor Megidish, nor anyone presenting entanglement swapping experiments presents anything like what Mjelva describes. His justification for a forward in time only hypothesis is flawed.

 

[DrChinese]

See equations 5a-5d in Mjelva. Projection onto states like these will correctly predict experimental results. These states have no entangled 1 & 4 pairs.

Mjelva's 4.1.1 analysis is quite general. I have applied this to the cases where Alice and Bob measure photon polarization in the H/V or L/R basis, which greatly simplifies things.

Mjelva's mistake is the assumption he uses to get his (4). That's where he asserts the system is in 1 of 4 equally probable states. The initial system is actually only in the state:

|Ψ->₁₂ ⊗ |Ψ->₃₄

Which is a product state of 2 entangled states. His leap to his (4) is exactly where his assumption can be tested experimentally. We simply start with any of those, and perform a BSM on 2 & 3. It's that simple, and he simply overlooked this possibility.

 

[Morbert]

Mjelva's mistake is the assumption he uses to get his (4). That's where he asserts the system is in 1 of 4 equally probable states. The initial system is actually only in the state:

|Ψ->₁₂ ⊗ |Ψ->₃₄

Which is a product state of 2 entangled states. His leap to his (4) is exactly where his assumption can be tested experimentally. We simply start with any of those, and perform a BSM on 2 & 3. It's that simple, and he simply overlooked this possibility.

Mjelva's (4) is a mixture of fours states that Alice's and Bob's irreversible measurements can project the initial state onto. If Alice and Bob do not first measure 1 & 4, then (4) would not be correct. But in delayed choice experiments like Ma's, they do, and hence (4) is correct, and Mjelva uses it to represents of a sample of runs. It reproduces all correlations and frequencies observed in the actual experiment, and the same procedure can be used to reproduce all correlations in any modification of the experiment (say, replacing the entangled states in the initial state with separable states).

Similarly, you can apply the standard forward-in-time unitary evolution + state reduction to calculate probabilities for the outcomes of individual runs, and arrive at the same correct numbers. E.g. If Alice and Bob measure in the R/L basis and get the results LL (and hence project photons 2 & 3 onto |RR〉₂₃), then we know Victor cannot obtain the result Φ+, as ⟨Φ+|RR〉₂₃ = 0. This is indeed a correlation observed in the actual experiment, and we can compute any such quantity for any set of possible outcomes recorded by Alice Bob and Victor.

 

[DrChinese]

Mjelva's (4) is a mixture of fours states that Alice's and Bob's irreversible measurements can project the initial state onto. If Alice and Bob do not first measure 1 & 4, then (4) would not be correct. But in delayed choice experiments like Ma's, they do, and hence (4) is correct, and Mjelva uses it to represents of a sample of runs. It reproduces all correlations and frequencies observed in the actual experiment, and the same procedure can be used to reproduce all correlations in any modification of the experiment (say, replacing the entangled states in the initial state with separable states).

Similarly, you can apply the standard forward-in-time unitary evolution + state reduction to calculate probabilities for the outcomes of individual runs, and arrive at the same correct numbers. E.g. If Alice and Bob measure in the R/L basis and get the results LL (and hence project photons 2 & 3 onto |RR〉₂₃), then we know Victor cannot obtain the result Φ+, as ⟨Φ+|RR〉₂₃ = 0. This is indeed a correlation observed in the actual experiment, and we can compute any such quantity for any set of possible outcomes recorded by Alice Bob and Victor.

State evolution, according to you/Mjelva:

1. Initially:
   |Ψ>₁₂₃₄ = |Ψ->₁₂⊗|Ψ->₃₄ is the starting state (also agreed by Ma).
2. |Ψ>₁₂₃₄ = (|LR>₁₂+|RL>₁₂)⊗(|LR>₃₄+|RL>₃₄) also shows the entanglement of pairs 1 & 2 and 3 & 4. Nothing controversial here.
   
   After Alice & Bob measure:
3. |Ψ>₁₂₃₄ = |R>₁⊗|L>₂⊗|L>₃⊗|R>₄ is the state immediately after 1 & 4 are measured and found to be |RR>, per your example. This is simply one of the 4 possibilities per the mixture of Mjelva's (pre-4, showing all four individually) and (4, shown as a "proper mixture"), expressed on the R/L basis.
   This is our point of departure. I say that there is no such |Ψ>₁₂₃₄ state as Mjelva's (4) until and unless all 4 are measured. I.e. there is no mixture of unentangled (4-fold separable) intermediate representations of |Ψ>₁₂₃₄ prior to an executed BSM.
4. |Ψ>₁₂₃₄ = |R>₁⊗(|H>₂+|V>₂)⊗(|H>₃+|V>₃)⊗|R>₄ is equivalent to 3. It shows the 2, 3 photons in a superposition on the H/V basis. At this point, we could be describing any 4 individual photons in the entire universe, as they are all in a Product (separable) State and there is no entanglement between any two.
   
   After BSM performed on 2 & 3 on the H/V basis:
5. The BSM in fact entangles them (2 & 3) in one of 4 Bell states, since they are now indistinguishable on that basis. Per Mjelva: "We observe that each of these joint states is a product state of the state of particle 1, the state of particle 4, and the [entangled] state of the pair 2, 3".
6. |Ψ>₁₂₃₄ = |R>₁⊗(½(|ψ+>₂₃-|ψ->₂₃-|Φ+>₂₃+|Φ->₂₃))⊗|R>₄ is therefore the actual post BSM state, in which |Φ+>₂₃ is non-zero.

If you started with 3., which can be arranged by the "Ma-X" technique I described in post #86: You would in fact evolve to 6. The actual experimental result of that yields equal numbers of |Φ+>₂₃ and |Φ->₂₃ instead of your |Φ+>₂₃=0. We know that with certainty for the reasons already explained, see point 3 in post #95. But, if you start with 1.: you never get to 3. in actual entanglement experiments. That step is skipped, and the evolution proceeds as described in Ma's (2). That's why those swapping experiments produce the expected quantum results.

Surely you can see the contradictions here. You are using the EPR reasoning to infer an "element of reality" to the intermediate state of 3. That hypothetical intermediate state does NOT produce the desired entanglement swapping results, therefore it cannot describe reality. A BSM evolves the state from Ma's (1) to Ma's (2) regardless of the timing of measurements by Alice and Bob. Which is a disproof of Mjelva's premise of a forward in time only description of entanglement swapping.

 

[DrChinese]

At this point, @Morbert must be asking something like: "Wait a minute! If DrChinese is correct* about Mjelva's evolution per his post #112, then how does Mjelva get to the same correct prediction for the swapping results as per Ma's experiment?"

Fair question. The answer (I will present specifically in my next post) is that Mjelva makes a second mistake that reverses his first mistake. That first mistake having been identified in point 3. of my post.


*That Mjelva's hypothetical forward in time only evolution is contradicted by experiment.

 

[DrChinese]

As mentioned in my previous post: Mjelva makes a second mistake in his state evolution that reverses his first. I know what his first error is, and I know he fixes it by the end, so the second should be easy to troubleshoot. It's easier to demonstrate this with his state evolution for the Megidish experiment, see diagram in Figure 1. We will contrast that with Mjelva's pre-(8), (8), and (9). His pre-(8) is wrong*, but his (9) is correct and is in line with Megidish's experimental results. So we need only look from pre-(8) to (8), or (8) to (9), to locate the second error.

The issue is that after a BSM on photons 2 & 3, they are cast into one of the 4 Bell states as shown in Mjelva's (8). However, his presentation of photon 4 is incorrect. I will re-cast the bases to match what Morbert and I have been using.

1. After our |R>₁ outcome for Alice:
|Ψ>₁₂₃₄
= |RL>₁₂ ⊗ |Ψ->₃₄
= |R>₁ ⊗ ½(|H>₂+|V>₂) ⊗ ½(|HV>₃₄-|VH>₃₄)
... and making explicit that there is no correlation whatsoever between an |R>₁ result and any future measurement or projection on photon 2's H/V basis. That, as I have said previously, is canonical.

2. And after the BSM:
|Ψ>₁₂₃₄
= |R>₁ ⊗ ¼(|ψ+>₂₃-|ψ->₂₃-|Φ+>₂₃+|Φ->₂₃) ⊗ ½(|L>₄+|R>₄)
... and likewise making explicit that there is no correlation whatsoever between any of the 4 entangled Bell states for photons 2 & 3, and any future measurement on photon 4's R/L basis. Photon 4 is now in a superposition in the R/L basis. This is what he should have been presented; for if he had, Mjevla wouldn't think he had matched the correct quantum prediction.

3. And we can now plainly see photons 1 & 4 have no correlation whatsoever, under a proper rendering of Mjelva's evolution.
So Mjelva deftly inserts that required (but non-existent) correlation when he goes from (8) to (9) by simply dropping all the terms in which we don't get the expected outcome of |RR>₁₄. (That includes dropping the term with |RR>₁₄ and |Φ+>₂₃.) And that is how the earlier error is fixed.** Regardless, (9) does not follow from his pre-(8) states using his own assumptions. So (9) is itself correct, but for the wrong reasons.

I'm sorry to report to Mjelva: In my opinion, a single paper has 2 critical mistakes; they negate the relevant conclusions.


*We know this per my 3. in post #112. After a measurement by Alice, photons 1 & 2 are NOT in a state like Mjelva's (pre-8): |Ψ>₁₂ = |Up Down>₁₂+|Down Up>₁₂ - not unless and until they are both observed as such.

**Or you could simply say he assumes what he seeks to prove.

 

[Sambuco]

Mjelva (and Morbert) claim there is a forward in time only evolution of quantum states that provides a viable description of swapping experiments.

Don't forget me! I'm on the @Morbert (and Mjelva) team. After all, I shared Mijelva's paper for some reason

As mentioned in my previous post: Mjelva makes a second mistake in his state evolution that reverses his first.

@DrChinese I find it difficult to follow your reasoning. In post #112 you critized Mjelva's eq. (4) and, since he finally got a result that agrees with the experiment, you try to find what the second error is that compensates for the first one. However, in post #114, you mentioned eqs. (8) and pre-(8). What confuses me is that eq. (4) correspond to Ma's experiment, while eqs. (8) and pre-(8) correspond to Megidish's experiment. In other words, if eq. (4) was wrong, the second error should be somewhere before eq. (7), because this is the point where the (projection-based) analysis of Ma's experiment ends.

Lucas.

 

[DrChinese]

Don't forget me! I'm on the @Morbert (and Mjelva) team. After all, I shared Mijelva's paper for some reason


@DrChinese I find it difficult to follow your reasoning. In post #112 you critized Mjelva's eq. (4) and, since he finally got a result that agrees with the experiment, you try to find what the second error is that compensates for the first one. However, in post #114, you mentioned eqs. (8) and pre-(8). What confuses me is that eq. (4) correspond to Ma's experiment, while eqs. (8) and pre-(8) correspond to Megidish's experiment. In other words, if eq. (4) was wrong, the second error should be somewhere before eq. (7), because this is the point where the (projection-based) analysis of Ma's experiment ends.

Lucas.

Wouldn’t want to forget you!

There are 2 problems in the Mjelva paper, and similar in Morberts analysis. Both of them can be seen in either his Ma treatment or Megidish treatment. It’s just convenience as to which is used. They are all equivalent. If you tell me which one to focus on, I’ll be glad to. I didn’t go to the Ma treatment for the second error because Mjelva made an unnecessary trip down Bayes Theorem, and that literally has nothing to do with quantum mechanics. So skip that.

What you have to understand is that a Nobel prize winner wrote a paper with Ma and they present the correct evolution. Morberts is flat out contradictory. So that should be a red flag to anyone. That experiment was done over a decade ago, and still stands. So everything I am saying is simply the same criticism they would be making.

There is no concept similar to Mjelva’s at work. The only thing driving it is a passionate desire to cling to Einsteinian causality. Which obviously QM does not respect.

 

[Morbert]

Segments in bold are my emphasis, and mark disagreements.

State evolution, according to you/Mjelva:

1. Initially:
   |Ψ>₁₂₃₄ = |Ψ->₁₂⊗|Ψ->₃₄ is the starting state (also agreed by Ma).
2. |Ψ>₁₂₃₄ = (|LR>₁₂+|RL>₁₂)⊗(|LR>₃₄+|RL>₃₄) also shows the entanglement of pairs 1 & 2 and 3 & 4. Nothing controversial here.

|R〉 = (|H〉 + i|V〉)/√2
|L〉 = (|H〉 - i|V〉)/√2
so
|Ψ-〉 = i(|RL〉 - |LR〉)/√2
so I work out the initial state to be
|Ψ-〉₁₂⊗|Ψ-〉₃₄ = -(|RL〉₁₂-|LR〉₁₂)⊗(|RL〉₃₄-|LR〉₃₄)/2

After Alice & Bob measure:
3. |Ψ>₁₂₃₄ = |R>₁⊗|L>₂⊗|L>₃⊗|R>₄ is the state immediately after 1 & 4 are measured and found to be |RR>, per your example. This is simply one of the 4 possibilities per the mixture of Mjelva's (pre-4, showing all four individually) and (4, shown as a "proper mixture"), expressed on the R/L basis.
This is our point of departure. I say that there is no such |Ψ>₁₂₃₄ state as Mjelva's (4) until and unless all 4 are measured. I.e. there is no mixture of unentangled (4-fold separable) intermediate representations of |Ψ>₁₂₃₄ prior to an executed BSM.
4. |Ψ>₁₂₃₄ = |R>₁⊗(|H>₂+|V>₂)⊗(|H>₃+|V>₃)⊗|R>₄ is equivalent to 3. It shows the 2, 3 photons in a superposition on the H/V basis. At this point, we could be describing any 4 individual photons in the entire universe, as they are all in a Product (separable) State and there is no entanglement between any two.

|Ψ〉₁₂₃₄
= |R〉₁⊗|L〉₂⊗|L〉₃⊗|R〉₄
= |R〉₁⊗(|H〉₂-i|V〉₂)⊗(|H〉₃-i|V〉₃)⊗|R〉₄/2

After BSM performed on 2 & 3 on the H/V basis:
5. The BSM in fact entangles them (2 & 3) in one of 4 Bell states, since they are now indistinguishable on that basis. Per Mjelva: "We observe that each of these joint states is a product state of the state of particle 1, the state of particle 4, and the [entangled] state of the pair 2, 3".
6. |Ψ>₁₂₃₄ = |R>₁⊗(½(|ψ+>₂₃-|ψ->₂₃-|Φ+>₂₃+|Φ->₂₃))⊗|R>₄ is therefore the actual post BSM state, in which |Φ+>₂₃ is non-zero.

If you started with 3., which can be arranged by the "Ma-X" technique I described in post #86: You would in fact evolve to 6. The actual experimental result of that yields equal numbers of |Φ+>₂₃ and |Φ->₂₃ instead of your |Φ+>₂₃=0. We know that with certainty for the reasons already explained, see point 3 in post #95. But, if you start with 1.: you never get to 3. in actual entanglement experiments. That step is skipped, and the evolution proceeds as described in Ma's (2).

|Ψ〉₁₂₃₄
= |R〉₁⊗|L〉₂⊗|L〉₃⊗|R〉₄
= |R〉₁⊗(|H〉₂-i|V〉₂)⊗(|H〉₃-i|V〉₃)⊗|R〉₄/2
= |R〉₁⊗(|HH〉₂₃-|VV〉₂₃-i|HV〉₂₃-i|VH〉₂₃)⊗|R〉₄/2
= |R〉₁⊗(|Φ-〉₂₃-i|Ψ+〉₂₃)⊗|R〉₄/√2

Note that this expansion only contains the Bell states |Φ-〉₂₃ and |Ψ+〉₂₃, hence |Φ+〉₂₃ is not a possible outcome. This is how the expected correlations are obtained in standard forward-in-time analysis of Ma's experiment. Each possible combination of outcomes for Alice and Bob will project onto a state that will restrict outcomes for Victor.

That's why those swapping experiments produce the expected quantum results.

As an aside: What Ma did in his paper was perfectly correct. It can be the case that both Ma's and Mjelva's approaches get the right results.

[edit] - Fixed math error.

 

[Morbert]

What you have to understand is that a Nobel prize winner wrote a paper with Ma and they present the correct evolution. Morberts is flat out contradictory. So that should be a red flag to anyone. That experiment was done over a decade ago, and still stands. So everything I am saying is simply the same criticism they would be making.

Nothing I have said contradicts the Ma paper. Mjelva's and Ma's analyses obtain the same results. Ma does not present a forward-in-time analysis because that is not the purpose of his paper.

 

[DrChinese]

DrChinese: Great, this is a good representation of the issues. My comments in italics below...

1. Agreed, and your last line's state is an Product State of 2 Entangled ones.

|Ψ-〉₁₂⊗|Ψ-〉₃₄ = -(|RL〉₁₂-|LR〉₁₂)⊗(|RL〉₃₄-|LR〉₃₄)/2

2. Product States below are NOT the state after measurements by Alice and Bob on your 1. After all, it is not entangled! This is error #1. However, it is a viable state that can be created. It is exactly what happens if you use my Ma-X method using Ma's type II PDC. Simply prevent polarization entanglement by failing to perform a key step in the normal process. You will get the Product State exactly as you have written. So we will continue using this as the starting state, instead of 1.

|Ψ〉1234
= |R〉1⊗|L〉2⊗|L〉3⊗|R〉4
= |R〉1⊗(|H〉2-i|V〉2)⊗(|H〉3-i|V〉3)⊗|R〉4/2

3. This does follow from the previous state.

|Ψ〉₁₂₃₄
= |R〉₁⊗(|H〉₂-i|V〉₂)⊗(|H〉₃-i|V〉₃)⊗|R〉₄/2

4. Your final line is error #2. You assume that which you seek to prove - by dropping the "offending" terms without justification.

|Ψ〉₁₂₃₄
= |R〉₁⊗(|HH〉₂₃-|VV〉₂₃-i|HV〉₂₃-i|VH〉₂₃)⊗|R〉₄/2
= |R〉₁⊗(|Φ-〉₂₃-i|Ψ+〉₂₃)⊗|R〉₄/√2

5. Note that this expansion only contains the Bell states |Φ-〉₂₃ and |Ψ+〉₂₃, hence |Φ+〉₂₃ is not a possible outcome. This is how the expected correlations are obtained in standard forward-in-time analysis of Ma's experiment. Each possible combination of outcomes for Alice and Bob will project onto a state that will restrict outcomes for Victor.

6. It can be the case that both Ma's and Mjelva's approaches get the right results.

1.-4. my comments above.

5. Exactly, you made the answer match the actual results - by using a "cheat" (don't take offence - it's just a word). Ma has nothing like this manipulation in their work on entanglement. Nobody else in the experimental world does either. And neither do accepted theoreticians such as Peres, Zeilinger, Gisin, etc.

The key to understanding error #2: Your 2. is a state that is easily implemented for verification one way or the other. When you start with this state, you actually get results that are diametrically opposite of what you wrongly claim. |Φ+〉₂₃ IS an equal outcome to |Φ-〉₂₃.

How do we know this? It is exactly what happens if you use my Ma-X method using Ma's type II PDC. Simply prevent polarization entanglement by failing to perform a key step in the normal process. You will get the Product State exactly as you have written. The step to skip: overlapping the Vertical and Horizontal cones during PDC. You will get a photon pair with known polarization. That leads to the Product State of your 2. But when you perform a BSM, the final results don't justify your final manipulation. Falsification by experiment.

If what I say weren't true, then there would certainly be no need to overlap the V/H cones in actual experimental production of the |Ψ-> pairs used in Ma (and many others). i) A lot of effort goes into overlapping the cones to make the V and H photons indistinguishable. ii) And that requirement significantly reduces the production rate.

You have yet to explain why they do this, and I have. They do this work because without that overlap, the pairs produce cannot be used for entanglement swapping precisely because they are in the Product State of your 2.

6. It could have been, and it did take me a bit of effort to see why his math seemed to mimic Ma. But now it’s clear why Mjelva is mistaken.

@Sambuco Does this make sense now?

 

[Morbert]

2. Product States below are NOT the state after measurements by Alice and Bob on your 1. After all, it is not entangled! This is error #1. However, it is a viable state that can be created. It is exactly what happens if you use my Ma-X method using Ma's type II PDC. Simply prevent polarization entanglement by failing to perform a key step in the normal process. You will get the Product State exactly as you have written. So we will continue using this as the starting state, instead of 1.

The product states are the states after measurement by Alice and Bob. This follows from standard QM when a forward-in-time analysis is applied, and is in agreement with experiment.

4. Your final line is error #2. You assume that which you seek to prove - by dropping the "offending" terms without justification.

No term is dropped. It follows from textbook QM and basic substitution. The relevant Bell states are

|Φ-〉= (|HH〉-|VV〉)/√2
|Ψ+〉= (|HV〉+|VH〉)/√2

so

|Ψ〉₁₂₃₄
= |R〉₁⊗|L〉₂⊗|L〉₃⊗|R〉₄
= |R〉₁⊗(|H〉₂-i|V〉₂)⊗(|H〉₃-i|V〉₃)⊗|R〉₄/2
= |R〉₁⊗(|HH〉₂₃-|VV〉₂₃-i|HV〉₂₃-i|VH〉₂₃)⊗|R〉₄/2
= |R〉₁⊗(|Φ-〉₂₃-i|Ψ+〉₂₃)⊗|R〉₄/√2

I invite anyone to check this step to the last line, where the 2 & 3 terms in brackets are:
[|HH〉₂₃-|VV〉₂₃-i|HV〉₂₃-i|VH〉₂₃]/2 = [ ( |HH〉₂₃-|VV〉₂₃ )/√2 - i( |HV〉₂₃+|VH〉₂₃ )/√2 ]/√2 = [|Φ-〉₂₃-i|Ψ+〉₂₃]/√2

This consistent with experiment, where the Φ- set has correlation in the R/L basis (see Ma's Fig 3) while the Φ+ set has anticorrelation in the R/L basis.