Dassinia
- 141
- 0
Hello
1. Homework Statement
Find the Fourier coefficients in the annulus problem of the text.
uxx+uyy=0 in 0<a²<x²+y²<b²
u=g(θ) for x²+y²=a²
u=h(θ) for x²+y²=b²
The solution is
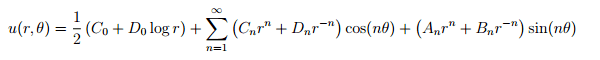
I have the solutions but when I solved it for Co and Do I didn't get the same thing, but or all the other coefficients I got the right thing.
Here is the problem
To get Co and Do I did the integral on both sides from 0 to 2π to get rid of the sum.
So I ended up with
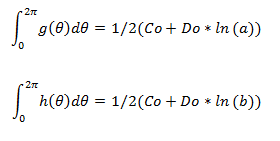
But the solution give a factor 1/π Before the integral of h and g , why ?
Thank you !
1. Homework Statement
Find the Fourier coefficients in the annulus problem of the text.
uxx+uyy=0 in 0<a²<x²+y²<b²
u=g(θ) for x²+y²=a²
u=h(θ) for x²+y²=b²
Homework Equations
The solution is
The Attempt at a Solution
I have the solutions but when I solved it for Co and Do I didn't get the same thing, but or all the other coefficients I got the right thing.
Here is the problem
To get Co and Do I did the integral on both sides from 0 to 2π to get rid of the sum.
So I ended up with
But the solution give a factor 1/π Before the integral of h and g , why ?
Thank you !