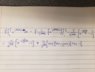Why Multiply by Exponential Terms in Fourier Series Calculations?
- Context: Engineering
- Thread starter lottotlyl
- Start date
Click For Summary
SUMMARY
The discussion centers on the application of exponential terms in Fourier series calculations, specifically addressing the use of the complex identity equation for sin(pi*k/3). The fundamental theorem of calculus is referenced, emphasizing the importance of integrating functions to derive solutions. The conversation highlights the necessity of multiplying by the term e^{(-jπk/3)} to simplify calculations, demonstrating a critical step in the Fourier series process.
PREREQUISITES- Understanding of Fourier series and their applications
- Familiarity with complex analysis concepts
- Knowledge of the fundamental theorem of calculus
- Basic algebraic manipulation skills
- Study the application of complex identities in Fourier series
- Learn about the fundamental theorem of calculus in depth
- Explore advanced topics in complex analysis
- Research the significance of exponential terms in signal processing
Mathematicians, physicists, engineers, and students involved in signal processing or Fourier analysis will benefit from this discussion.
Similar threads
Engineering
Fourier transform of a shifted sine wave
- · Replies 3 ·
- · Replies 3 ·
- · Replies 3 ·
- · Replies 26 ·
- · Replies 4 ·
- · Replies 3 ·
- · Replies 1 ·
- · Replies 6 ·