ymnoklan said:
Top: at equilibrium
Middle: spring pulled to the left
Bottom: spring pulled to the right
What do you think of this?
Here are some comments. Note: I’m in the UK - there may be some variations with how FBDs are drawn in your country.
__________________
General Comments
1. Can you rotate the image so it’s easier for us to read?
2. You are asked for the FBD of the cylinder. The
only object shown in each FBD should be the cylinder. If the long horizontal line on each diagram is meant to be the rod, it should be removed.
3. ##G## is not the usual symbol for weight (here in the UK, anyway). I’d use ##W## but maybe this is related to language.
4. Include a ‘key’ which explains each force. E.g.
##\vec G## weight of cylinder
##\vec N## <your description of what you think ##\vec N## is>
##\vec F## <your description of what you think ##\vec F## is>
Apologies - I didn't notice that you had done this below the diagrams.
5. On a FBD, distributed forces (forces not acting at a point) are usually shown as a
single arrow, So,rather than 2 arrows for ##\vec N##, use a single arrow in the middle. (In the same way that a single arrow is used for weight, even though gravity acts on every atom in the cylinder.)
(Note: engineers may sometimes use a series of arrows for a distributed force ##\uparrow \uparrow \uparrow \uparrow##. But I assume we’re talking physics here, not engineering.)
__________________
Digram 1
Looks like you’ve got the total length of the ##N## arrows correct. Good. But they need replacing with a single arrow (item 5, above).
__________________
Digrams 2 and 3
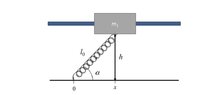
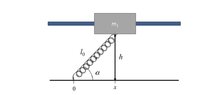
At equilibrium, the spring is angled, ##\alpha \approx 45^o## (see Post 6 diagram).
For a small left-displacement of the cylinder, say to make ##\alpha= 50^o##, the spring will be in a state of
compression; so what is the direction on the force on the spring? For a small displacement right, say to make ##\alpha = 40^o##, the spring will be in a state of tension and will
not be as shown in your diagram 3!
The dotted lines are not needed. In fact they show the y-component of ##\vec F## to be equal to the weight – which is is not generally true.
Using the approximate length of an arrow to indicate the magnitude of each force, it appear that there is a net downwards force-component on the cylinder. This would causes downwards acceleration – but the cylinder does not accelerate downwards!
Edited - LaTeX and other corrections.