Frequency Response of a Damped Car-Suspension System

[Engineer47]

Homework Statement

How can I solve for the frequency response of a damped system when I have the full matrices for M, C, and K when a car suspension hits a pot-hole of a certain height?

Relevant Equations

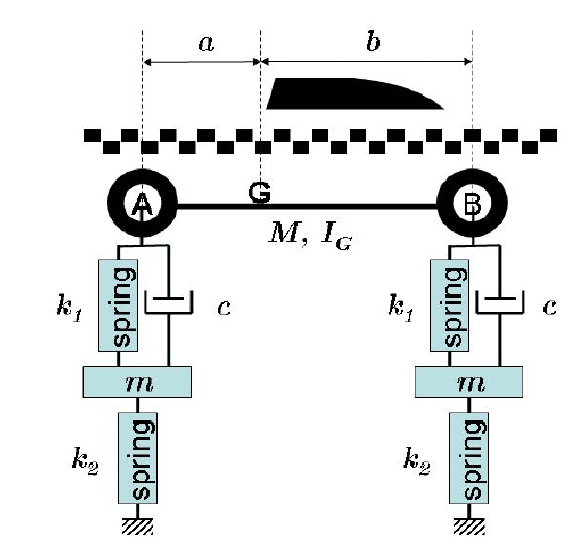
The equation I have now to work with it M(U(double dot)) which is a 4x4 matrix, times a 4x1 matrix, -[K]*[U] -[C][U(dot)] where M is the mass matrix, k is the spring matrix, and c is the damper matrix, all of the same dimensions as the M and U(double dot) matrix above. I am trying to solve using eigenvalues or vectors I believe with modal superposition on Matlab!

The quarter car system is represented by the above picture and I currently have all of the equations of motion and constants for each spring, mass, damper, distance, and moment of inertia. How can I find the frequency response with this information and knowing both tires hit a pothole of height h at the same time? Thanks!

 

[BvU]

Helllo engineer, !

Looks more like a half-car representation to me
Even so, your wheels (front and back) won't hit the pothole simultaneously -- or is that outside the scope of your exercise ? And you draw an $a$ and a $b$ -- but do you have the moment of inertia around a wheel as a given ?

Anyway: what happens at a pothole is not described with a frequency response, but with a step response (or a pulse ersponse, but both: in the time domain, not the frequency domain.

Did you learn about Laplace transforms already ? If not, you have to solve the differential equation as is.

 

[Engineer47]

Helllo engineer, !

Looks more like a half-car representation to me
Even so, your wheels (front and back) won't hit the pothole simultaneously -- or is that outside the scope of your exercise ? And you draw an $a$ and a $b$ -- but do you have the moment of inertia around a wheel as a given ?

Anyway: what happens at a pothole is not described with a frequency response, but with a step response (or a pulse ersponse, but both: in the time domain, not the frequency domain.

Did you learn about Laplace transforms already ? If not, you have to solve the differential equation as is.

Hi! It technically is a half-car representation, and is to be treated as a rigid body. Furthermore, the moment of inertia of the wheels aren't given and can be neglected. I already have the equations of motion of each mass as well, I am just unsure on how to take those and see how a pothole affects them. And although it makes sense that the front and back wheels wouldn't hit the hole at the same time, I am to assume it is. And although I have learned about Laplace Transforms already, I think the problem requires some use of ODE45 in MATLAB and solve for undamped modes, finding the modal weights, and then summing to find the frequency response to all of the modes!