Friction acting on rolling wheel

[mbrmbrg]

Homework Statement

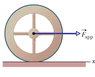
In Figure 11-30(see attatched), a constant horizontal force F_app of magnitude 12 N is applied to a wheel of mass 8 kg and radius 0.70 m. The wheel rolls smoothly on the horizontal surface, and the acceleration of its center of mass has magnitude 0.75 m/s2.

(a) In unit-vector notation, what is the frictional force on the wheel?
[? Ni]
(b) What is the rotational inertia of the wheel about the rotation axis through its center of mass?
[3.92 kg*m^2 ]

Homework Equations

\tau=r\times F

\tau=I\alpha

I_{hoop}=mr^2

\alpha=\frac{a_{com}}{r}

The Attempt at a Solution

I took the axis of rotation to be perpindicular to the wheel's center of mass.

There are four forces acting on the wheel: mg, normal, applied force, and friction. Of those four forces, only friction does not pass through the axis of rotation, so friction alone (symbol is lowercase f) contributes to torque.

\tau=r\times f=I\alpha
fr=(mr^2)(\frac{a_{com}}{r})
f=ma_{com}(\frac{r^2}{r^2})
f=(8kg)(.75m/s^2)=6N
BZZZZZ. I lose.

Though on the bright side, my solution for the rotational inertia earned me a pretty green check mark...

 

[Doc Al]

There are four forces acting on the wheel: mg, normal, applied force, and friction. Of those four forces, only friction does not pass through the axis of rotation, so friction alone (symbol is lowercase f) contributes to torque.

All good.

Don't assume that the wheel can be modeled as a thin ring of mass. Instead, apply Newton's 2nd law twice: Once for rotation; once for translation (what's the net force on the wheel?). Combine those two equations to solve for f and I.

 

[mbrmbrg]

Don't assume that the wheel can be modeled as a thin ring of mass.

But doing so gave me the correct rotational inertia...
Whoa, cool! solving for friction using translation then using that still gives me the right inertia! So neat when the physics works!

Instead, apply Newton's 2nd law twice: Once for rotation; once for translation (what's the net force on the wheel?). Combine those two equations to solve for f and I.

Using only translation, I solved for friction, and got the answer WebAssign wanted: -6N. But that gives friction pointing away from the direction of the overall motion of the wheel; it had taken me so long to comprehend that friction points in the same direction in which the body rolls!

Thanks!

 

[Doc Al]

But that gives friction pointing away from the direction of the overall motion of the wheel; it had taken me so long to comprehend that friction points in the same direction in which the body rolls!

I hope you now realize that the friction force does not point in the same direction as the applied force. The wheel accelerates to the right, but friction acts to the left.

 

[Slepton]

Interesting. What if there was a blockade of some height (less than the radius of the wheel) was on its way? On that case how should one calculate the minimum force so as to just lift the wheel off the ground ? Any idea ?

 

[Doc Al]

Interesting. What if there was a blockade of some height (less than the radius of the wheel) was on its way? On that case how should one calculate the minimum force so as to just lift the wheel off the ground ? Any idea ?

Consider torques about the edge of the step it must get over.

 

[Slepton]

Hi Doc Al, could you explain a bit more ? Thanks

 

[Doc Al]

Consider the forces acting on the wheel. For the wheel to get over the block or step, you must exert enough upward torque to balance out the downward torque due to gravity.