Fullwave Rectifier: Calculate Peak Diode Current

  • Thread starter Thread starter exis
  • Start date Start date
  • Tags Tags
    Rectifier
Click For Summary

Discussion Overview

The discussion revolves around calculating the peak diode current in a full-wave rectifier circuit fed by a 50V peak AC signal. Participants explore the implications of various assumptions, such as the voltage drop across the diodes and the behavior of the capacitor in the circuit. The context includes theoretical calculations and practical considerations related to the circuit's performance.

Discussion Character

  • Homework-related
  • Mathematical reasoning
  • Debate/contested

Main Points Raised

  • One participant calculates the peak diode current assuming ideal diodes with zero voltage drop, yielding a value of 11.6mA based on the formula I_max = V_peak / R.
  • Another participant questions the assumption of zero voltage drop across the diodes, suggesting that a typical forward voltage drop of 0.6 to 0.7V should be considered.
  • A participant mentions that their calculated peak diode current does not match an expected value of 127mA, indicating a potential oversight in their calculations.
  • Discussion includes the need to account for the current flowing into the capacitor during the voltage rise, which may affect the peak current calculations.
  • One participant provides an estimation of the peak-to-peak ripple voltage across the capacitor and discusses the discharge curve's behavior, suggesting a method to derive the peak capacitor current using the formula I(t) = C dv/dt.
  • Another participant reports a combined peak current of about 126mA, indicating a different approach or calculation method.

Areas of Agreement / Disagreement

Participants express differing views on the assumptions regarding diode voltage drop and the methods for calculating peak current. There is no consensus on the correct approach or final values, as multiple competing views remain present in the discussion.

Contextual Notes

Participants have not resolved the assumptions regarding the diode voltage drop, and there are varying interpretations of the capacitor's behavior in the circuit. The calculations depend on these assumptions, which remain unresolved.

exis
Messages
22
Reaction score
0

Homework Statement



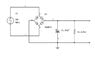
A 50V peak AC signal at 50Hz is fed to a 1:1 turns ratio transformer full-wave rectifier circuit. The full-wave rectifier waveform is smoothed by the use of a capacitor C=47uF, R=4.3kohms.

I need to calculate the peak diode current (however before this i was asked to calculate the average voltage across the load resistor R and the peak-peak rippe voltage across R)

The Attempt at a Solution



Vrippe(peak-peak) = Vpeak/(2fRC) = 50/(2*50*4300*47*10^-6) = 2.47V
Vdc = Vpeak - Vripple(peak-peak)/2 = 50 - 2.47/2 = 48.76V

I reasoned that the maximum current through the diode occurs when Vin=Vpeak. Therefore I_max=Vpeak/R=50/4300=11.6mA.

I tried considering the current through the capacitor as well but didnt know how to find the max current through it.
 

Attachments

  • circuit.jpg
    circuit.jpg
    10.8 KB · Views: 514
Physics news on Phys.org
Note: are you to assume the diodes have zero voltage across them, or would they have 0.6 to 0.7 V across them?

Once you answer that, the key here is: You know the peak voltage across the resistor. You know R for the resistor. Find I for the resistor.
 
I assumed the diodes are ideal, therefore zero voltage drop across them. I found the peak diode current exactly the way you just said and the answer I got isn't correct. Peak voltage = 50V, R=4300ohms, therefore I_max = 11.6mA. The answer i should be getting is 127mA
 
Weird. Perhaps you are also supposed to calculate a current going into the capacitor when the voltage increases from it's minimum to maximum values (i.e., the rising part of the ripple in the voltage).
 
I usually work these things by first guestimating then refining. The rough, peak-to-peak ripple is about 0.6 volts across the capacitor--very small.

The discharge curve is nearly a straight line and will intercept the rectified voltage curve very close to 90 degrees. About 81 degrees. From dv/dt, at this point on the curve, you can obtain the peak capacitor current.

I(t) = C dv/dt
 
btw, I get a combined peak current of about 126 mA
 
Phrak, how did you work it out exactly please?
 

Similar threads

Mean voltage and current, rectifiers
  • · Replies 3 ·
Replies
3
Views
2K
Engineering Rectifier Circuit - Guidance requested
  • · Replies 14 ·
Replies
14
Views
4K
Engineering Full wave Bridge rectifier and smoothing circuit
  • · Replies 11 ·
Replies
11
Views
6K
Resistive heating power AC vs rectified AC/DC
  • · Replies 10 ·
Replies
10
Views
5K
Engineering Calculating current and voltage of a rectifier circuit
  • · Replies 3 ·
Replies
3
Views
2K
How to Calculate Capacitor and Power Values in a Full Wave Rectifier Circuit
  • · Replies 17 ·
Replies
17
Views
4K
Calculating Voltage Ripple in a Full Wave Rectifier Circuit
  • · Replies 2 ·
Replies
2
Views
6K
Calculating Active Effect & Effect Factor for Alternating Current
  • · Replies 4 ·
Replies
4
Views
2K
Design Rectifier: Choose Transformer, Diode Config, Capacitor, Draw Waveforms
  • · Replies 27 ·
Replies
27
Views
11K
Designing a Voltage Regulated Power Supply
  • · Replies 1 ·
Replies
1
Views
4K