Lindsayyyy
- 215
- 0
Hi everyone,
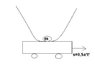
I have a mass like in the drawing and a moving cart with constant acceleration. The potential (also in the drawing) is given as V=A4x^{4}
I want to calculate the frequency of the oscillation of the mass as a function of the acceleration when the cart is moving.
Galilean transformation
Taylor series(?)
differential equation
F=-grad V (here F=-dV/dx)
Well, I'm stuck. I have a moving frame of referenca and a stagnant one. My problem is I have to find a equation of motion in order to find the frequency. I think I need to develop a harmonic potential via Taylor series. But I'm so unsure when it comes to transformations as I'm new into this. I don't know if I even have to transform the x in the potential equation or not and around which point I should make the Taylor series etc etc.
My attempt was to use the transformation:
x'=x+ \frac 1 2 a t^{2}
Is this even right? Do I have to put the x' in the equation for the potential? Then the potential depends on time aswell? Can someone help me out with this problem and give me any hints?
Thanks for your help
Homework Statement
I have a mass like in the drawing and a moving cart with constant acceleration. The potential (also in the drawing) is given as V=A4x^{4}
I want to calculate the frequency of the oscillation of the mass as a function of the acceleration when the cart is moving.
Homework Equations
Galilean transformation
Taylor series(?)
differential equation
F=-grad V (here F=-dV/dx)
The Attempt at a Solution
Well, I'm stuck. I have a moving frame of referenca and a stagnant one. My problem is I have to find a equation of motion in order to find the frequency. I think I need to develop a harmonic potential via Taylor series. But I'm so unsure when it comes to transformations as I'm new into this. I don't know if I even have to transform the x in the potential equation or not and around which point I should make the Taylor series etc etc.
My attempt was to use the transformation:
x'=x+ \frac 1 2 a t^{2}
Is this even right? Do I have to put the x' in the equation for the potential? Then the potential depends on time aswell? Can someone help me out with this problem and give me any hints?
Thanks for your help