Gas Expansion in insulated cylinder (piston & Diaphragm)

Click For Summary

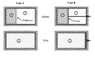
Discussion Overview

The discussion revolves around the analysis of gas expansion in an insulated cylinder divided by a diaphragm or a piston. Participants explore the thermodynamic implications of two cases: one involving a diaphragm (case A) and the other a piston (case B). The focus includes concepts of free expansion, work done on surroundings, and the nature of the processes involved, including isothermal and adiabatic conditions.

Discussion Character

  • Exploratory
  • Technical explanation
  • Debate/contested
  • Mathematical reasoning

Main Points Raised

  • Some participants question whether both cases can be classified as free expansion, particularly considering the nature of the piston in case B.
  • There is a discussion about the implications of a massless piston and whether it affects the expansion process.
  • Some participants propose that if the piston is connected to the outside, it would do work on the surroundings, altering the physics of the problem.
  • One participant suggests that case A is an irreversible free expansion process with no heat transfer or work done, leading to no change in internal energy and thus an isothermal process.
  • In contrast, case B is debated as potentially being an adiabatic expansion process, where work is done on the surroundings, and the final pressure is questioned.
  • Participants discuss the relationship between pressure, volume, and temperature changes in both cases, with some asserting that case B cannot be treated as free expansion.
  • There is uncertainty about whether case B can be assumed to be reversible, with some participants suggesting that the rate of expansion is a determining factor.
  • The ideal gas law is referenced to analyze the relationships between pressure, volume, and temperature in both cases.
  • Some participants express confusion regarding the temperature changes in case B compared to case A, particularly in relation to the nature of the expansion processes.

Areas of Agreement / Disagreement

Participants exhibit multiple competing views regarding the classification of the expansion processes, the implications of the piston being connected to the outside, and the nature of the temperature changes in both cases. The discussion remains unresolved with no consensus reached on several key points.

Contextual Notes

There are limitations regarding assumptions about the nature of the piston, the external conditions, and the definitions of free and adiabatic expansions. The discussion also reflects uncertainty about the rates of expansion and their impact on the reversibility of the processes.

pyroknife
Messages
611
Reaction score
4
I attached an image of two expansion cases I am analyzing. Both cases involve an insulated cylinder that is divided by a separating element (diaphragm for case A and piston for B). The portion on the right is evacuated. The left contains a calorically perfect gas with an initial pressure and temperature.

Case A is a thin diaphragm and at a certain point in time, it is suddenly removed (removed without friction&flow disturbance) and gas expands to fill the whole cylinder. Case B is a piston which is allowed to move (without friction) while gas expands to fill the whole cylinder.


Would both of these cases be considered free expansion?
 

Attachments

  • Untitled.png
    Untitled.png
    21.7 KB · Views: 608
Science news on Phys.org
Is the piston massive or massless? What difference does that make?
 
I believe it is massless. Being massless would imply it is free expansion?
 
A massless piston not backed by anything would not impede the expansion in any way.
 
voko said:
A massless piston not backed by anything would not impede the expansion in any way.

Got it. I was speaking to a professor about case B. He mentioned that the piston is connected to the outside. Does this change anything in the physics of the problem?
 
Most likely it does. What are your thoughts?
 
I am thinking that if it's connected to the outside it does work on the surroundings.
 
That's what I think, too.
 
Hmmm, I am trying to analyze which one of the cases would result in a higher final pressure.

For case A, I believe this is irreversible free expansion process, with no heat transfer and work, thus change in internal energy is zero. Since the system involves a perfect gas where internal energy is only a function of temperature, that would mean change in temperature is zero, making the process isothermal. Thus we can use the simple P1*V1=P2V2, where state 1 is the initial state and state 2 is the final state after the gas expands to cover up the whole cylinder.

For case B, I am a bit lost on how I can go about figuring out the final pressure. Would it be at constant process expansion since work is done on the surroundings?
For case B to expand, wouldn't heat need to be applied to the gas?
 
  • #10
I believe you need to assume that the gas can expand in case B without any external heat. I agree with your method for case A.
 
  • #11
Hmmm, I see. So the gas has to create a expansion force large enough to push the cylinder and expand?
 
  • #12
Yes, it will have to do work on the surroundings.
 
  • #13
I made the assumption that case B was an adiabatic expansion process. So this means the pressure inside has to be larger than outside for it to be expanding. Case B is not free expansion.
If I were to obtain the final pressure for case B, would I have to apply the work equation?
I feel there is a much simpler way.
 
  • #14
pyroknife said:
I made the assumption that case B was an adiabatic expansion process. So this means the pressure inside has to be larger than outside for it to be expanding. Case B is not free expansion.
If I were to obtain the final pressure for case B, would I have to apply the work equation?

You won't be able to unless you know exactly what the "surroundings" are. But that is not required if you just need to state whether the final pressure is lower or greater than in case A.

You know that in case A ##p_1 V_1 = p_2^A V_2 ##. You know that in case B you will have some ##p_2^B##. What do you know about ##p_2^B## without going into details of the process, and knowing solely that some work is done?
 
  • #15
Does your subscript 2 represent the properties associated with the initially evacuated volume or the final state after the gas expansion?
 
  • #16
Since the initial volume has to have a smaller pressure in order for the gas filled volume to expand, that means in the final state, the pressure of the gas should be lowered because work is done on the surroundings.
 
  • #17
Subscript 2 means "final state" (same as in #9 I believe).

Your logic in #16 is not flawless. Take again you reasoning from #9. We know that ##V_2 > V_1##, so ##p_1 V_1 = p_2 V_2 ## implies that ## p_2 < p_ 1 ## even though no work has been done (this ## p_2 ## is what I denoted as ##p_2^A##).
 
  • #18
Is there a formatting issue in your last post? If not, your post appears to be displaying wrong for me.
 
  • #19
I do not see any problem there. What seems wrong?
 
  • #20
voko said:
I do not see any problem there. What seems wrong?

I refreshed it and it looks fine now. It looked weird earlier (see attached).

I can no longer use the relationship P1V1=P2V2 because this is no longer an isothermal process and thus, there is a change in temperature.
 

Attachments

  • Untitled.png
    Untitled.png
    11.4 KB · Views: 497
  • #21
pyroknife said:
I can no longer use the relationship P1V1=P2V2 because this is no longer an isothermal process and thus, there is a change in temperature.

What change? Does it increase or decrease? Why?
 
  • #22
voko said:
What change? Does it increase or decrease? Why?

I think I can answer your question by looking at the ideal gas equation, but I would like to understand it from a more conceptual point of view.

From the ideal gas equation we have P1V1/T1=P2V2/T2. For the gas to expand, P1 has to be greater than the surroundings. So pressure must decrease. Then that means temperature must decrease.
 
  • #23
That could also be said in case A. Yet in case A temperature is constant.
 
  • #24
voko said:
That could also be said in case A. Yet in case A temperature is constant.

Sorry. I was having a dumb moment. I forgot all about volume. Let me think.
 
  • #25
Another question I had (which may help with answering the pressure problem) is if this scenario can be assumed as reversible. I think this cannot be determined because we do not know the rate of expansion? The rate of expansion should be quite low for it to be considered reversible.
 
  • #26
You are overthinking the problem. Answer the questions from #21. Compare with case A. Use the ideal gas law.
 
  • #27
Hmmm, in case A, the pressure and volume change. In case B, the pressure, temperature, and volume change.
We know volume increases for both cases, but I am not sure how to think about the physical process associated with the pressure and temperature change?
For the gas to expand, the pressure must be greater than the surroundings. For some reason, I am thinking that the work done on the surroundings is solely associated with the increase in volume at a constant pressure.
 
  • #28
Once again. You have established that in case A, temperature is constant. Why?

What does that mean with regard to temperature in case B?
 
  • #29
voko said:
Once again. You have established that in case A, temperature is constant. Why?

What does that mean with regard to temperature in case B?


Temperature is constant because there is no change in temperature for the free expansion of a perfect gas.

Case B is not free expansion, therefore the same principle does not hold true. Should I be thinking of this in a different way? I'm not sure how the case A scenario would help in understanding case B's temperature change.
 
  • #30
pyroknife said:
Temperature is constant because there is no change in temperature for the free expansion of a perfect gas.

Why is there no change in temperature in this case?

Case B is not free expansion, therefore the same principle does not hold true.

Consequently, what happens with temperature?
 

Similar threads

Graduate Work done during adiabatic expansion on piston
  • · Replies 8 ·
Replies
8
Views
4K
High School Quasistatic condition for a process involving a piston in a cylinder
  • · Replies 1 ·
Replies
1
Views
2K
High School Gas cylinder at constant pressure being exposed to atmosphere, how?
  • · Replies 8 ·
Replies
8
Views
3K
Graduate Thermodynamics: Gas Expansion with Piston Friction
  • · Replies 65 ·
3
Replies
65
Views
79K
Undergrad Work in hydrostatic system in cylinder with piston: P_int or P_ext?
  • · Replies 5 ·
Replies
5
Views
2K
Undergrad Irreversible adiabatic processes & entropy change (clarification needed)
  • · Replies 22 ·
Replies
22
Views
6K
Undergrad Calculating Cooling Effect in Gas Cylinder Expansion
  • · Replies 5 ·
Replies
5
Views
4K
Undergrad Sign convention on work done to a closed system containing gas
  • · Replies 5 ·
Replies
5
Views
3K
Undergrad Yet again about (real) gas compression
  • · Replies 20 ·
Replies
20
Views
3K
Undergrad The relationship between reversible and irreversible processes
  • · Replies 5 ·
Replies
5
Views
2K