- #1
Const@ntine
- 285
- 18
Homework Statement
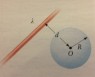
A charged, straight line/rod of infinite length has a Discrete uniform distribution of charge, has a linear density of λ and is at a distance d from a sphere with a radius of R.
Find the entirety of the Electrical Flux that is caused by this charged rod, which passes through the surface of the sphere.
a) When R < d
b) When R > d
Homework Equations
[/B]
ΦΕ = ∫E→⋅dA→ (for a surface)
ΦΕ = qinternal/ε0 (Gauss' Law)
E = ke∫(dq/r2)r∧ (the r here is a Euclidean Vector)
λ = Q/l
The Attempt at a Solution
a) Okay, so we know that we have an Electrical Flux only when there is a charge inside the sphere/surrounding shape, because otherwise all the lines of the Electric Field go through one point of the shape, and leave through another, resulting in ΦΕ = 0.
Because R < d, the rod/line is outside the sphere, and thus what we described above happens.
β) Here's where I'm stuck. My initial idea was:
-I'll find E.
-Then I'll use the ΦΕ = ∫E→⋅dA→ (for a surface)
Problem is, I'm not sure how to tackle the finding E part. All the exercises I did on that part where with a straight rod on the x axis. Basically I'm having trouble with doing the integration at E = ke∫dq/r2r∧
I'm having a bit of trouble with all the integrals and whatnot here, so I could use a nudge or two. Electrics is entirely new to me so I don't have anywhere to run back to, like with previous semesters.
Any help is appreciated!