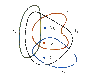Gauss's Law and electric flux of a surface

[Keithkent09]

Four closed surfaces, S1 through S4, together with the charges -2Q, Q, and -Q are sketched in the figure below. (The colored lines are the intersections of the surfaces with the page.) Find the electric flux through each surface. (Use Q for the charge Q and epsilon_0 for 0.)
(Picture Attached)

2.
Electric Flux= the integral of EdA=q/epsilon_0


3.
All that I could think to do was set q=the charge of the inside of the desired surface. I was not sure how I could quantitatively define how the different charges within the surfaces affected each other.

 

[dacruick]

Gauss` law is your best friend. the flux through a surface will only be non zero if there is a charge inside that surface. think about putting an imaginary sphere in the middle of a river. All the water that runs into the sphere also runs out of it. Having a charge inside the surface is like putting a sprinkler inside your imaginary sphere. Now the amount of water in is 0, and the amount of water out is this analogy`s version of flux.

So any surface with no charge inside, has 0 flux.

This principle is displayed simply in your equations for flux. where flux is = to
charge enclosed / epsilon naught.

So your flux for the red surface with Q and -2Q, it will have a flux of -Q/epsilon naught

 

[kerimek]

I would approach this problem by first defining the parameters and variables involved. In this case, we have four closed surfaces, S1 through S4, with charges -2Q, Q, and -Q. We also have the value of epsilon_0, which is the permittivity of free space. The figure also shows the intersections of the surfaces with the page, which can help us visualize the problem.

Next, I would use Gauss's Law to determine the electric flux through each surface. Gauss's Law states that the electric flux through a closed surface is equal to the charge enclosed by that surface divided by epsilon_0. In other words, the electric flux is directly proportional to the charge enclosed by the surface.

To find the electric flux through each surface, we can use the formula: Electric Flux = (charge enclosed)/epsilon_0. We know that the charge enclosed by each surface is equal to the charge within that surface, so we can simply plug in the values of -2Q, Q, and -Q for each surface and solve for the electric flux.

For S1, the electric flux would be (Q+(-2Q))/epsilon_0 = -Q/epsilon_0.
For S2, the electric flux would be (-2Q+Q)/epsilon_0 = -Q/epsilon_0.
For S3, the electric flux would be (-Q+(-2Q))/epsilon_0 = -3Q/epsilon_0.
For S4, the electric flux would be (Q+(-Q))/epsilon_0 = 0.

Therefore, the electric flux through S1 and S2 would be the same, -Q/epsilon_0, while the electric flux through S3 would be -3Q/epsilon_0 and the electric flux through S4 would be 0.

In conclusion, by using Gauss's Law and understanding the relationship between electric flux and the charge enclosed by a surface, we can calculate the electric flux through each of the four surfaces in the given figure. This approach is based on scientific principles and allows us to quantitatively define and solve the problem.