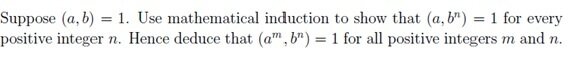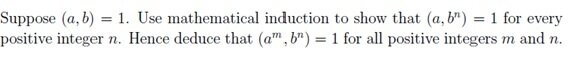- #1
GCD Proving Assistance - Get Help Now!
- MHB
- Thread starter Joe20
- Start date
-
- Tags
- Gcd
In summary: The base case could be $(a,b)=1$, and the inductive step could be proving that $(a,b^n) = 1 for every positive integer $n$.
- #2
Greg
Gold Member
MHB
- 1,378
- 0
Hello Alexis87 and welcome to MHB! :D
We ask that our users show their progress (work thus far or thoughts on how to begin) when posting questions. This way our helpers can see where you are stuck or may be going astray and will be able to post the best help possible without potentially making a suggestion which you have already tried, which would waste your time and that of the helper.
Can you post what you have done so far?
We ask that our users show their progress (work thus far or thoughts on how to begin) when posting questions. This way our helpers can see where you are stuck or may be going astray and will be able to post the best help possible without potentially making a suggestion which you have already tried, which would waste your time and that of the helper.
Can you post what you have done so far?
- #3
Joe20
- 53
- 1
Thanks for the advise. I have no idea how to start.
- #4
I like Serena
Homework Helper
MHB
- 16,336
- 258
We're talking about a proof by induction.
That means that the proof starts with a base case, which is followed by an induction hypothesis.
What could the base case be?
That means that the proof starts with a base case, which is followed by an induction hypothesis.
What could the base case be?
- #5
Opalg
Gold Member
MHB
- 2,778
- 13
A few hints to get you started:Alexis87 said:
The neatest way to work with GCDs is to use the fact that the condition for $(a,b) = 1$ is that there exist integers $x,y$ such that $ax+by=1$.
Suppose that condition holds. Then (multiplying through by $by$) it follows that $axby + b^2y^2 = by = 1-ax.$ Therefore $$a(xby + x) + b^2y^2 = 1.$$ That equation is of the form $aX + b^2Y = 1$, which shows that $(a,b^2) = 1.$
Can you use that as the basis for an inductive proof that $(a,b^n) = 1$ for all $n$?
Attachments
- #6
Evgeny.Makarov
Gold Member
MHB
- 2,436
- 4
I think the basis for an induction proof that $(a,b^n)=1$ for every positive integer $n$ is $(a,b)=1$ and not $(a,b^2)=1$.Opalg said:
- #7
Opalg
Gold Member
MHB
- 2,778
- 13
Yes, of course. But I was not implying that the base case should be $(a,b^2)=1$. What I was suggesting was a technique that might be used for proving the inductive step.Evgeny.Makarov said:
FAQ: GCD Proving Assistance - Get Help Now!
What is GCD Proving Assistance?
GCD Proving Assistance is a program designed to help individuals prove their greatest common divisor (GCD) calculations. It is specifically tailored for those who are struggling with understanding or proving their GCD calculations, providing step-by-step assistance and guidance.
How does GCD Proving Assistance work?
GCD Proving Assistance uses a combination of algorithms and mathematical principles to analyze and verify GCD calculations. Users can input their steps and the program will check for any errors or provide suggestions for improvement. It also offers explanations and tips to help users understand the process better.
Is GCD Proving Assistance free to use?
Yes, GCD Proving Assistance is completely free to use. It was created with the intention of helping individuals improve their understanding of GCD calculations, so there is no cost associated with using the program.
Can GCD Proving Assistance be used for all types of GCD calculations?
Yes, GCD Proving Assistance can be used for all types of GCD calculations, including simple and complex ones. It is designed to be flexible and adaptable, so it can handle a wide range of GCD problems.
Will GCD Proving Assistance solve the calculation for me?
No, GCD Proving Assistance is not a calculator or a solving tool. It is meant to assist and guide users in understanding and proving their own GCD calculations. Users still need to input their own steps and the program will only provide feedback and suggestions.