- 37,382
- 14,215
- TL;DR Summary
- Solution to a long-standing problem: How to make lenses without spherical abberation?
Publication: Rafael G. González-Acuña and Héctor A. Chaparro-Romo, "General formula for bi-aspheric singlet lens design free of spherical aberration," Appl. Opt. 57, 9341-9345 (2018)
Open access preprint: arXiv
Given one surface of a lens, how does the other surface has to look like to avoid spherical abberation? A question as old as the design of lenses. Computers found numerical approximations but an analytic expression is new. Just use this handy formula:
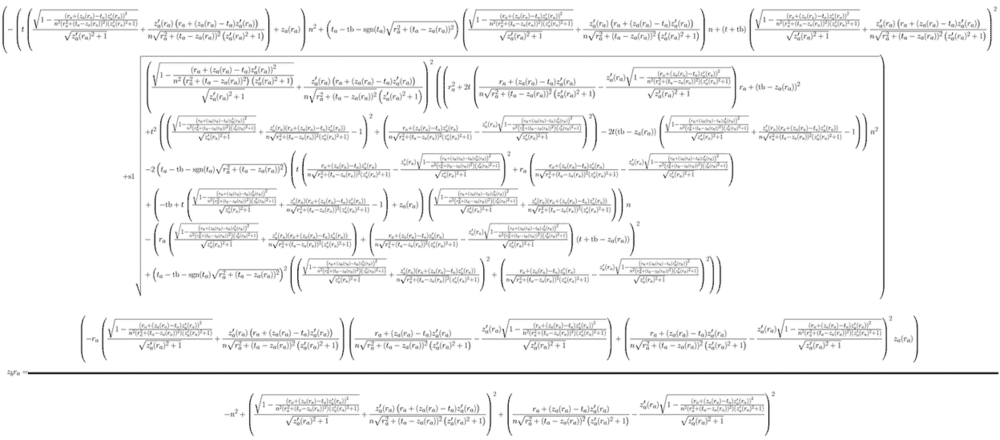
Open access preprint: arXiv
Given one surface of a lens, how does the other surface has to look like to avoid spherical abberation? A question as old as the design of lenses. Computers found numerical approximations but an analytic expression is new. Just use this handy formula: